Baire classes
Families of real functions which are defined inductively using the ordinal number of limit transitions involved in the definition of the function, and which constitute the classification of functions proposed in 1899 by R. Baire [1], known as the Baire classification. The set of all continuous functions  , where
, where  is a metric space, is called the zero-th Baire class
is a metric space, is called the zero-th Baire class  . The first Baire class
. The first Baire class  is the set of discontinuous functions
is the set of discontinuous functions  which are the limit of a sequence of continuous functions converging at each point. The Baire class
which are the limit of a sequence of continuous functions converging at each point. The Baire class  , where
, where  is an ordinal number of the first or second class, is defined as the set of functions
is an ordinal number of the first or second class, is defined as the set of functions  which do not form part of any of the preceding classes, but which may be represented as
which do not form part of any of the preceding classes, but which may be represented as  , where
, where  ,
, 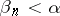 . The union of the Baire classes
. The union of the Baire classes  over all ordinal numbers of the first and second class constitutes the set of Baire functions. This is the minimal class of functions
over all ordinal numbers of the first and second class constitutes the set of Baire functions. This is the minimal class of functions  containing all the continuous functions and closed with respect to pointwise convergence. A linear combination, product and quotient (for non-zero denominators) of functions of a Baire class not higher than
containing all the continuous functions and closed with respect to pointwise convergence. A linear combination, product and quotient (for non-zero denominators) of functions of a Baire class not higher than  is a function in a Baire class not higher than
is a function in a Baire class not higher than  . A uniformly convergent sequence of functions of a Baire class not higher than
. A uniformly convergent sequence of functions of a Baire class not higher than  has as limit a function in a Baire class not higher than
has as limit a function in a Baire class not higher than  . Necessary and sufficient conditions have been established for a sequence of functions in a Baire class not higher than
. Necessary and sufficient conditions have been established for a sequence of functions in a Baire class not higher than  to converge to a function in a Baire class not higher than
to converge to a function in a Baire class not higher than  [4]. The union of all dense-in-itself sets
[4]. The union of all dense-in-itself sets  is called the kernel of the topological space
is called the kernel of the topological space  . If
. If 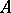 is a complete space with a non-empty dense-in-itself kernel, none of the Baire classes is empty [2]. The set of Baire functions coincides with the set of Borel-measurable functions (cf. Borel measure), and for this reason they are all Lebesgue-measurable (cf. Lebesgue measure). A Lebesgue-measurable function
is a complete space with a non-empty dense-in-itself kernel, none of the Baire classes is empty [2]. The set of Baire functions coincides with the set of Borel-measurable functions (cf. Borel measure), and for this reason they are all Lebesgue-measurable (cf. Lebesgue measure). A Lebesgue-measurable function  is equivalent to a Baire function of a Baire class not higher than two [3]. Baire, who considered functions defined on
is equivalent to a Baire function of a Baire class not higher than two [3]. Baire, who considered functions defined on  (mainly on
(mainly on  ), made the most detailed study of functions of the first class. He showed that a necessary and sufficient condition for a discontinuous function to belong to the first class is the existence of a point of continuity of the induced function on each perfect set (Baire's theorem). This theorem is applicable to a function
), made the most detailed study of functions of the first class. He showed that a necessary and sufficient condition for a discontinuous function to belong to the first class is the existence of a point of continuity of the induced function on each perfect set (Baire's theorem). This theorem is applicable to a function  if
if  has the Baire property [2]. The concept of a Baire function can be naturally generalized to functions
has the Baire property [2]. The concept of a Baire function can be naturally generalized to functions  , where
, where 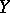 is an arbitrary metric space.
is an arbitrary metric space.
References
| [1] | R. Baire, "Leçons sur les fonctions discontinues, professées au collège de France" , Gauthier-Villars (1905) |
| [2] | F. Hausdorff, "Grundzüge der Mengenlehre" , Leipzig (1914) (Reprinted (incomplete) English translation: Set theory, Chelsea (1978)) |
| [3] | I.P. Natanson, "Theorie der Funktionen einer reellen Veränderlichen" , H. Deutsch , Frankfurt a.M. (1961) (Translated from Russian) |
| [4] | B.M. Gagaeff, "Sur les suites convergentes de fonctions mesurables  " Fund. Math. , 18 (1932) pp. 182–188 " Fund. Math. , 18 (1932) pp. 182–188 |
Comments
A subset of a topological space is called dense-in-itself if it has no relatively-isolated points. A modern English reference for the notion of Baire classes is [a1]. For an introduction to the topic and some applications, cf. [a2].
References
| [a1] | A.C.M. van Rooy, W.H. Schikhof, "A second course on real functions" , Cambridge Univ. Press (1982) |
| [a2] | R.P Boas jr., "A primer of real functions" , Math. Assoc. Amer. (1981) |
Baire classes. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Baire_classes&oldid=12977