BMOA-space
space of analytic functions of bounded mean oscillation
In 1961, F. John and L. Nirenberg [a4] introduced the space of functions of bounded mean oscillation,  , in their study of differential equations (cf. also
, in their study of differential equations (cf. also  -space). About a decade later, C. Fefferman proved his famous duality theorem [a1] [a2], which states that the dual of the Hardy space
-space). About a decade later, C. Fefferman proved his famous duality theorem [a1] [a2], which states that the dual of the Hardy space  is
is  (cf. also Hardy spaces).
(cf. also Hardy spaces).
In these early works,  was studied primarily as a space of real-valued functions, but Fefferman's result raised questions about the nature of analytic functions in the Hardy spaces of the unit disc whose boundary values are in
was studied primarily as a space of real-valued functions, but Fefferman's result raised questions about the nature of analytic functions in the Hardy spaces of the unit disc whose boundary values are in  . This is the definition of
. This is the definition of  and the duality theorem provides the alternative that
and the duality theorem provides the alternative that  consists of those analytic functions that can be represented as a sum of two analytic functions, one with a bounded real part and the other with a bounded imaginary part (cf. also Analytic function; Hardy spaces).
consists of those analytic functions that can be represented as a sum of two analytic functions, one with a bounded real part and the other with a bounded imaginary part (cf. also Analytic function; Hardy spaces).
Ch. Pommerenke [a5] proved that a univalent function is in 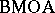 if and only if there is a bound on the radius of the discs contained in the image. Subsequently, W. Hayman and Pommerenke [a3] and D. Stegenga [a7] proved that any analytic function is in
if and only if there is a bound on the radius of the discs contained in the image. Subsequently, W. Hayman and Pommerenke [a3] and D. Stegenga [a7] proved that any analytic function is in 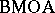 provided the complement of its image is sufficiently thick in a technical sense that uses the notion of logarithmic capacity. As an example, any function whose image does not contain a disc of a fixed radius
provided the complement of its image is sufficiently thick in a technical sense that uses the notion of logarithmic capacity. As an example, any function whose image does not contain a disc of a fixed radius  centred at
centred at 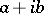 , where
, where  ,
, 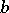 range over all integers, satisfies this criterion and hence is in
range over all integers, satisfies this criterion and hence is in 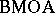 .
.
In a similar vein, K. Stephenson and Stegenga [a6] proved that an analytic function is in 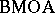 provided its image Riemann surface (viewed as spread out over the complex plane) has the following property: There are
provided its image Riemann surface (viewed as spread out over the complex plane) has the following property: There are 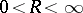 ,
, 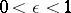 so that a Brownian traveller will, with probability at least
so that a Brownian traveller will, with probability at least  , fall off the edge of the surface before travelling outward
, fall off the edge of the surface before travelling outward  units (cf. also Brownian motion). As an example, an overlapping infinite saussage-shaped region can be constructed so that the Riemann mapping function maps onto to the entire complex plane but is nevertheless in
units (cf. also Brownian motion). As an example, an overlapping infinite saussage-shaped region can be constructed so that the Riemann mapping function maps onto to the entire complex plane but is nevertheless in  .
.
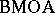 comes up naturally in many problems in analysis, such as on the composition operator, the corona problem (cf. also Hardy classes), and on functions in one and several complex variables.
comes up naturally in many problems in analysis, such as on the composition operator, the corona problem (cf. also Hardy classes), and on functions in one and several complex variables.  and its variants has become an indispensable tool in real and complex analysis.
and its variants has become an indispensable tool in real and complex analysis.
References
| [a1] | C. Fefferman, "Characterization of bounded mean oscillation" Bull. Amer. Math. Soc. , 77 (1971) pp. 587–588 |
| [a2] | C. Fefferman, E. Stein, "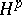 spaces of several variables" Acta Math. , 129 (1974) pp. 137–193 spaces of several variables" Acta Math. , 129 (1974) pp. 137–193 |
| [a3] | W. Hayman, Ch. Pommerenke, "On analytic functions of bounded mean oscillation" Bull. London Math. Soc. , 10 (1978) pp. 219–224 |
| [a4] | F. John, L. Nirenberg, "On functions of bounded mean oscillation" Commun. Pure Appl. Math. , 14 (1961) pp. 415–426 |
| [a5] | Ch. Pommerenke, "Schlichte Funktionen und analytische Funktionen von beschränkter mittlerer Oszillation" Comment. Math. Helv. , 152 (1977) pp. 591–602 |
| [a6] | K. Stephenson, D. Stegenga, "A geometric characterization of analytic functions of bounded mean oscillation" J. London Math. Soc. (2) , 24 (1981) pp. 243–254 |
| [a7] | D. Stegenga, "A geometric condition that implies BMOA" , Proc. Symp. Pure Math. , XXXV:1 , Amer. Math. Soc. (1979) pp. 427–430 |
BMOA-space. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=BMOA-space&oldid=17734