BGG resolution
The structure of a real Lie group 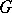 can be studied by considering representations of the complexification
can be studied by considering representations of the complexification 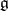 of its Lie algebra (cf. also Representation of a Lie algebra). These are viewed as left modules over the universal enveloping algebra
of its Lie algebra (cf. also Representation of a Lie algebra). These are viewed as left modules over the universal enveloping algebra 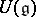 of
of 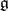 , or
, or 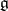 -modules. The Lie algebras
-modules. The Lie algebras  considered here are the complexifications of real semi-simple Lie algebras corresponding to real, connected, semi-simple Lie groups. A Cartan subalgebra
considered here are the complexifications of real semi-simple Lie algebras corresponding to real, connected, semi-simple Lie groups. A Cartan subalgebra 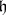 , that is, a maximal Abelian subalgebra with the property that its adjoint representation on
, that is, a maximal Abelian subalgebra with the property that its adjoint representation on 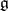 is semi-simple, is chosen (cf. also Cartan subalgebra). A root system
is semi-simple, is chosen (cf. also Cartan subalgebra). A root system 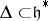 , corresponding to the resulting decomposition of
, corresponding to the resulting decomposition of 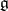 , is obtained. A further choice of a positive root system
, is obtained. A further choice of a positive root system 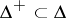 determines subalgebras
determines subalgebras  and
and 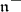 corresponding to the positive and negative root spaces, respectively. The building blocks in the study of
corresponding to the positive and negative root spaces, respectively. The building blocks in the study of 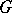 are the finite-dimensional irreducible
are the finite-dimensional irreducible 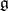 -modules
-modules 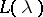 . They are indexed by the set
. They are indexed by the set 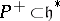 of dominant integral weights
of dominant integral weights 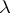 relative to
relative to 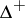 .
.
For any ring 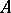 with unity, a resolution of a left
with unity, a resolution of a left 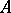 -module
-module 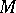 is an exact chain complex of
is an exact chain complex of 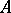 -modules:
-modules:
 |
For example, let  be a complex Lie algebra, and let
be a complex Lie algebra, and let 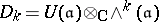 , where
, where 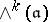 is the
is the 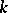 th exterior power of
th exterior power of  ,
, 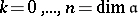 . Let
. Let
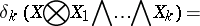 |
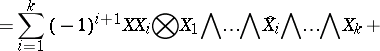 |
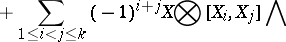 |
 |
where 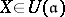 ,
, 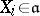 and
and 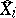 means that
means that 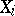 has been omitted. Let
has been omitted. Let 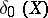 be the constant term of
be the constant term of 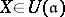 . Then
. Then
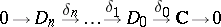 |
is the standard resolution 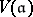 of the trivial
of the trivial  -module
-module 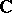 . If
. If 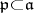 is a subalgebra, one considers the relative version
is a subalgebra, one considers the relative version 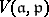 of
of 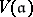 by setting
by setting 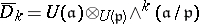 . One observes that the obvious modification of the
. One observes that the obvious modification of the 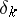 produces mappings
produces mappings 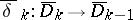 ,
, 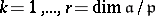 , and that the resulting complex is similarly exact.
, and that the resulting complex is similarly exact.
In [a3] two constructions of a resolution of  ,
, 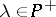 , were obtained. They are described below.
, were obtained. They are described below.
Weak BGG resolution.
Let  and let
and let  be the category of finitely-generated
be the category of finitely-generated 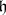 -diagonalizable
-diagonalizable 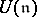 -finite
-finite 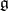 -modules ([a2]). Let
-modules ([a2]). Let 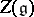 denote the centre of
denote the centre of 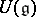 . If M is a
. If M is a 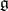 -module, let
-module, let 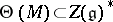 denote the set of eigenvalues of
denote the set of eigenvalues of 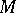 . For
. For 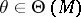 , let
, let  denote the eigenspace associated to
denote the eigenspace associated to 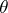 . The set
. The set  consists of only one element, denoted by
consists of only one element, denoted by 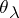 . For
. For 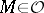 ,
, 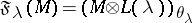 defines an exact functor in
defines an exact functor in 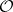 . If
. If 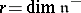 , let
, let
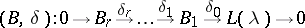 |
be the image of 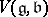 under the functor
under the functor 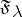 .
. 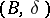 is known as the weak BGG resolution. Its importance lies in the property of the
is known as the weak BGG resolution. Its importance lies in the property of the 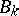 explained below. For
explained below. For 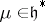 ,
, 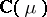 denotes the trivially extended action of
denotes the trivially extended action of 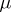 from
from 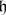 to
to 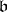 . The
. The 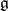 -module
-module 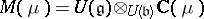 is the Verma module associated to
is the Verma module associated to 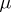 . Let
. Let 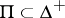 denote the set of simple (i.e. indecomposable in
denote the set of simple (i.e. indecomposable in 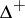 , positive roots. Let
, positive roots. Let 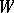 be the group of automorphisms of
be the group of automorphisms of 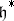 generated by the reflections
generated by the reflections 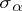 relative to
relative to 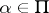 (cf. also Weyl group). Let
(cf. also Weyl group). Let 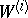 be the set of elements
be the set of elements 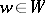 that are minimally expressed as a product of
that are minimally expressed as a product of 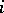 reflections
reflections 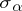 ,
,  . One writes
. One writes 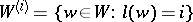 . Each
. Each 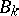 has a filtration (cf. also Filtered algebra)
has a filtration (cf. also Filtered algebra) 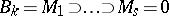 of
of 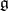 -modules such that
-modules such that  and
and 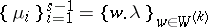 , where
, where 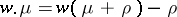 and
and 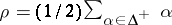 .
.
If  is a Lie algebra and
is a Lie algebra and
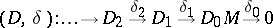 |
is a resolution of the  -module
-module 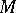 by projective
by projective  -modules, and
-modules, and 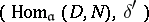 is the image of
is the image of 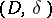 under the functor
under the functor 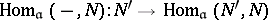 , then
, then 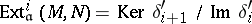 . The cohomology groups
. The cohomology groups 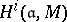 are defined as
are defined as 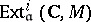 . If
. If 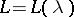 , and
, and 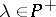 , the weak BGG resolution implies that
, the weak BGG resolution implies that 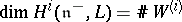 .
.
Strong BGG resolution.
For 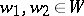 one writes
one writes 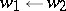 if there exists a
if there exists a 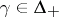 such that
such that 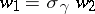 and
and 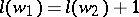 . This relation induces a partial ordering
. This relation induces a partial ordering 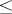 on
on 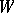 , by setting
, by setting  whenever there are
whenever there are  in
in 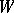 such that
such that 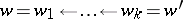 . It was shown in [a1] that
. It was shown in [a1] that
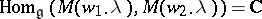 |
if and only if 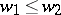 . Furthermore, every such homomorphism is zero or injective. One fixes, for each pair
. Furthermore, every such homomorphism is zero or injective. One fixes, for each pair 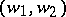 , one such injection
, one such injection 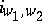 . Let
. Let 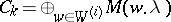 . Therefore, a
. Therefore, a 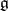 -homomorphism
-homomorphism 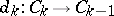 is determined by a complex matrix
is determined by a complex matrix 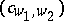 with
with 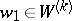 and
and 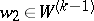 . It is shown in [a3] that there exist
. It is shown in [a3] that there exist 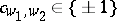 ,
, 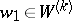 ,
, 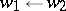 , for
, for 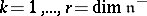 , such that
, such that
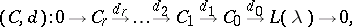 |
where 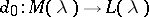 is the canonical surjection, is exact. This strong BGG resolution refines the weak BGG resolution
is the canonical surjection, is exact. This strong BGG resolution refines the weak BGG resolution 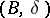 and, in particular, calculates the cohomology groups
and, in particular, calculates the cohomology groups 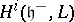 . In [a4] it was proved that the weak and the strong BGG resolutions are isomorphic. The results of [a4] apply to the more general situation of parabolic subalgebras
. In [a4] it was proved that the weak and the strong BGG resolutions are isomorphic. The results of [a4] apply to the more general situation of parabolic subalgebras 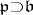 . They imply the existence of a complex in terms of the degenerate principal series representations of
. They imply the existence of a complex in terms of the degenerate principal series representations of 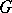 that has the same cohomology as the de Rham complex [a4]. The BGG resolution has been extended to Kac–Moody algebras (see [a5] and also Kac–Moody algebra) and to the Lie algebra of vector fields on the circle [a6].
that has the same cohomology as the de Rham complex [a4]. The BGG resolution has been extended to Kac–Moody algebras (see [a5] and also Kac–Moody algebra) and to the Lie algebra of vector fields on the circle [a6].
References
| [a1] | I.N. Bernstein, I.M. Gelfand, S.I. Gelfand, "Structure of representations generated by vectors of highest weight" Funkts. Anal. Prilozh. , 5 : 1 (1971) pp. 1–9 |
| [a2] | I.N. Bernstein, I.M. Gelfand, S.I. Gelfand, "A certain category of 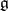 -modules" Funkts. Anal. Prilozh. , 10 : 2 (1976) pp. 1–8 -modules" Funkts. Anal. Prilozh. , 10 : 2 (1976) pp. 1–8 |
| [a3] | I.N. Bernstein, I.M. Gelfand, S.I. Gelfand, "Differential operators on the base affine space and a study of 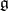 -modules" I.M. Gelfand (ed.) , Lie groups and their representations, Proc. Summer School on Group Representations , Janos Bolyai Math. Soc.&Wiley (1975) pp. 39–64 -modules" I.M. Gelfand (ed.) , Lie groups and their representations, Proc. Summer School on Group Representations , Janos Bolyai Math. Soc.&Wiley (1975) pp. 39–64 |
| [a4] | A. Rocha-Caridi, "Splitting criteria for 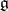 -modules induced from a parabolic and the Bernstein–Gelfand–Gelfand resolution of a finite dimensional, irreducible -modules induced from a parabolic and the Bernstein–Gelfand–Gelfand resolution of a finite dimensional, irreducible 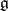 -module" Trans. Amer. Math. Soc. , 262 : 2 (1980) pp. 335–366 -module" Trans. Amer. Math. Soc. , 262 : 2 (1980) pp. 335–366 |
| [a5] | A. Rocha-Caridi, N.R. Wallach, "Projective modules over graded Lie algebras" Math. Z. , 180 (1982) pp. 151–177 |
| [a6] | A. Rocha-Caridi, N.R. Wallach, "Highest weight modules over graded Lie algebras: Resolutions, filtrations and character formulas" Trans. Amer. Math. Soc. , 277 : 1 (1983) pp. 133–162 |
BGG resolution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=BGG_resolution&oldid=14028