Bäcklund transformation
It was A.V. Bäcklund who, in 1873, 1880, 1882, and 1883 introduced transformations between pairs of surfaces 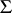 ,
, 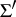 in
in 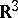 such that the surface element
such that the surface element
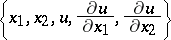 |
of 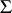 is connected to the surface element
is connected to the surface element
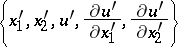 |
of 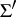 by four relations of the type
by four relations of the type
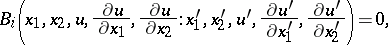 | (a1) |
where 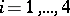 [a1], [a2]. Bäcklund transformations may be considered as generalized Lie–Bianchi transformations (cf. also Bianchi transformation). J. Clairin and E. Goursat extended Bäcklund's results [a1], [a2].
[a1], [a2]. Bäcklund transformations may be considered as generalized Lie–Bianchi transformations (cf. also Bianchi transformation). J. Clairin and E. Goursat extended Bäcklund's results [a1], [a2].
Application of the integrability condition
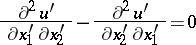 | (a2) |
leads, under certain circumstances, either to a pair of third-order equations or to a single second-order equation for  . The analogous integrability condition on the unprimed quantities leads, again under appropriate conditions, to a pair of third-order equations or to a single second-order equation for
. The analogous integrability condition on the unprimed quantities leads, again under appropriate conditions, to a pair of third-order equations or to a single second-order equation for 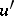 . In this case, implicit in the Bäcklund relations, (a1) is a mapping between the solutions
. In this case, implicit in the Bäcklund relations, (a1) is a mapping between the solutions 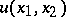 ,
, 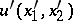 of generally distinct systems of partial differential equations. This can be used as follows: If the solution of the transformed equation or pair of equations is known, then the Bäcklund relations (a1) may be used to generate the solution of the original equation or pair of equations. If the equations are invariant under the Bäcklund transformation (a1), then the latter may be used to construct an infinite sequence of new solutions from a known trivial solution. Both types of Bäcklund transformations have important applications. Bäcklund transformations may also be used to link certain non-linear equations to canonical forms whose properties are well known.
of generally distinct systems of partial differential equations. This can be used as follows: If the solution of the transformed equation or pair of equations is known, then the Bäcklund relations (a1) may be used to generate the solution of the original equation or pair of equations. If the equations are invariant under the Bäcklund transformation (a1), then the latter may be used to construct an infinite sequence of new solutions from a known trivial solution. Both types of Bäcklund transformations have important applications. Bäcklund transformations may also be used to link certain non-linear equations to canonical forms whose properties are well known.
The classical Bäcklund transformation (a1) can be generalized to include second-order derivatives. Thus, transformations of the type
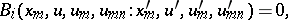 | (a3) |
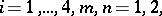 |
are introduced. These extensions of the Bäcklund transformation can be used to obtain Bäcklund solutions for the Korteweg–de Vries equation.
The jet-bundle formulation of Bäcklund transformations provides the best framework for a unified treatment of the subject [a1], [a3]. A number of interesting ordinary and partial differential equations admit Bäcklund and auto-Bäcklund transformations. They have been found to have applications in mathematical physics.
Examples of Bäcklund transformations.
See also [a1], [a3], [a4], [a5].
1) Consider the two non-linear ordinary differential equations
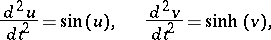 |
where  and
and  are real-valued functions. Then
are real-valued functions. Then
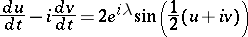 |
defines a Bäcklund transformation.
2) Consider the one-dimensional sine-Gordon equation in light-cone coordinates 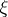 and
and 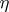 :
:
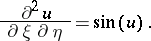 |
Then
 |
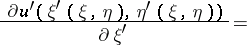 |
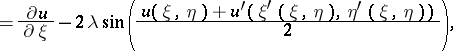 |
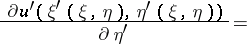 |
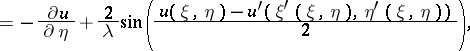 |
defines an auto-Bäcklund transformation, where 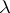 is a non-zero real parameter. A non-linear superposability principle can be given, whereby an infinite sequence of solutions may be constructed by purely algebraic means. A hierarchy of solutions can be found starting from the trivial solution
is a non-zero real parameter. A non-linear superposability principle can be given, whereby an infinite sequence of solutions may be constructed by purely algebraic means. A hierarchy of solutions can be found starting from the trivial solution 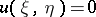 .
.
3) The Korteweg–de Vries equation
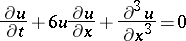 |
and the modified Korteweg–de Vries equation
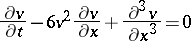 |
are related by the Miura transformation
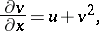 |
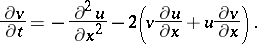 |
References
| [a1] | C. Rogers, W.F. Shadwick, "Bäcklund transformations and their applications" , Acad. (1982) |
| [a2] | R.L. Anderson, N.H. Ibragimov, "Lie–Bäcklund transformations in applications" , SIAM (Soc. Industrial Applied Math.) (1979) |
| [a3] | W.-H. Steeb, "Continuous symmetries, Lie algebras, differential equations and computer algebra" , World Sci. (1996) |
| [a4] | W.-H. Steeb, "Problems and solutions in theoretical and mathematical physics: Advanced problems" , II , World Sci. (1996) |
| [a5] | W.-H. Steeb, N. Euler, "Nonlinear evolution equations and Painlevé test" , World Sci. (1988) |
Bäcklund transformation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=B%C3%A4cklund_transformation&oldid=12607