Axiom of choice

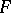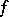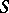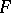One of the axioms in set theory. It states that for any family of non-empty sets there exists a function such that, for any set from , one has 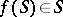( 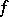is called a choice function on 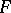). For finite families 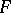the axiom of choice can be deduced from the other axioms of set theory (e.g. in the system ZF).

The axiom of choice was explicitly formulated by E. Zermelo (1904) and was objected to by many mathematicians. This is explained, first, by its purely existential character which makes it different from the remaining axioms of set theory and, secondly, by some of its implications which are "unacceptable" or even contradict intuitive "common sense" . Thus, the axiom of choice implies: the existence of a Lebesgue non-measurable set of real numbers; the existence of three subdivisions of the sphere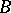

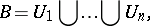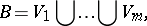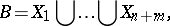such that 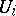is congruent with 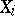, , 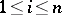and 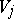is congruent with 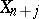, 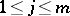. Thus, the sphere 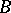is divisible into a finite number of parts 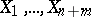which can be moved in space to form two spheres identical to it.

Many postulates equivalent to the axiom of choice were subsequently discovered. Among these are: 1) The well-ordering theorem: On any set 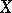there exists a total order 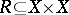such that any non-empty set 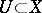contains a least element in the sense of the relation 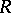; 2) the maximality principle (Zorn's lemma): If any totally ordered subset 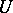of a partially ordered set 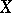is bounded from above, 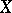contains a maximal element; 3) any non-trivial lattice with a unit element has a maximal ideal; 4) the product of compact topological spaces is compact; and 5) any set 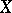has the same cardinality as .

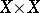The axiom of choice does not contradict the other axioms of set theory (e.g. the system ZF) and cannot be logically deduced from them if they are non-contradictory. The axiom of choice is extensively employed in classical mathematics. Thus, it is used in the following theorems. 1) Each subgroup of a free group is free; 2) the algebraic closure of an algebraic field exists and is unique up to an isomorphism; and 3) each vector space has a basis. It is also used in: 4) the equivalence of the two definitions of continuity of a function at a point (the 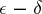-definition and the definition by limits of sequences) and in proving 5) the countable additivity of the Lebesgue measure. The last two theorems follow from the countable axiom of choice (the formulation of the axiom includes the condition of countability of the family 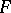). It was proved that the theorems 1) to 5) are not deducible in the system ZF if ZF is non-contradictory.

A model of set theory has been constructed which meets the countable axiom of choice and in which each set of numbers is Lebesgue-measurable. This model was constructed on the assumption that the system ZF does not contradict the axiom of the existence of an inaccessible cardinal number.

References

[1]	A. Levy, "Foundations of set theory" , North-Holland (1973)
[2]	T.J. Jech, "Lectures in set theory: with particular emphasis on the method of forcing" , Lect. notes in math. , 217 , Springer (1971)
[3]	T.J. Jech, "The axiom of choice" , North-Holland (1973)

References

[a1]	T.J. Jech, "Set theory" , Acad. Press (1978) (Translated from German)