Average

with weight 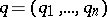, , 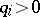, 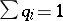of a set of real numbers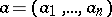

A variable

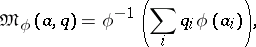where 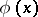is a continuous strictly-monotone function on 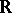. When 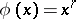, one obtains

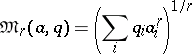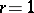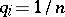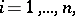
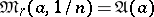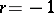and, in particular, when , , will be the arithmetic average of the numbers , while when , it will be the harmonic average. The concepts of the geometric average 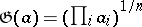and the weighted geometric average

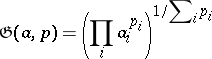are introduced separately.

One of the basic results of the theory of averages is the inequality 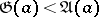, except when all 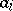are equal to each other. Other results are:

1) ;

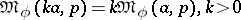2) 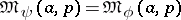if and only if , , ;

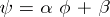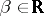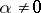3) 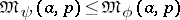if and only if 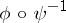is a convex function; in particular 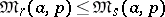if .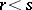

The concept of an average can be extended to infinite sequences under the assumption that the corresponding series and products converge, and to other functions. The following is such an example:

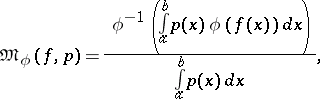given the condition that almost everywhere on the corresponding interval and that 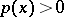. Thus,

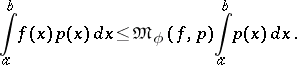References

[1]	G.H. Hardy, J.E. Littlewood, G. Pólya, "Inequalities" , Cambridge Univ. Press (1934)

Comments

Instead of "average" the term "meanmean" is also quite often used: arithmetic mean, geometric mean, etc.

References

[a1]	D.S. Mitrinović, "Analytic inequalities" , Springer (1970)
[a2]	D.S. Mitrinović, "Elementary inequalities" , Noordhoff (1964)