Automorphic form
A meromorphic function on a bounded domain 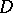 of the complex space
of the complex space  that, for some discrete group of transformations
that, for some discrete group of transformations  operating on this domain, satisfies an equation:
operating on this domain, satisfies an equation:
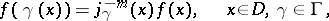 |
Here  is the Jacobian of the mapping
is the Jacobian of the mapping 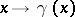 and
and  is an integer known as the weight of the automorphic form. If the group
is an integer known as the weight of the automorphic form. If the group  acts fixed-point free, then automorphic forms define differential forms on the quotient space
acts fixed-point free, then automorphic forms define differential forms on the quotient space  and vice versa. Automorphic forms may be used in the construction of non-trivial automorphic functions (cf. Automorphic function). It has been shown that if
and vice versa. Automorphic forms may be used in the construction of non-trivial automorphic functions (cf. Automorphic function). It has been shown that if 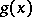 is a function that is holomorphic and bounded on a domain
is a function that is holomorphic and bounded on a domain 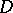 , then the series
, then the series
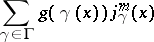 |
converges for large values of 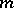 , thus representing a non-trivial automorphic function of weight
, thus representing a non-trivial automorphic function of weight 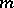 . These series are called Poincaré theta-series.
. These series are called Poincaré theta-series.
The classical definition of automorphic forms, given above, has recently served as the starting point of a far-reaching generalization in the theory of discrete subgroups of Lie groups and adèle groups.
References
| [1] | H. Poincaré, , Oeuvres de H. Poincaré , Gauthier-Villars (1916–1965) |
| [2] | C.L. Siegel, "Automorphe Funktionen in mehrerer Variablen" , Math. Inst. Göttingen (1955) |
Comments
References [a2] and [a3] can serve to get some idea of modern developments and topics in the theory of automorphic forms and its relations with other parts of mathematics. (Cf. the comments to the article Automorphic function for a more general notion).
References
| [a1] | W.L. Baily jr., "Introductory lectures on automorphic forms" , Iwanami Shoten & Princeton Univ. Press (1973) |
| [a2] | A. Borel (ed.) W. Casselman (ed.) , Automorphic forms, representations and 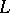 -functions , Proc. Symp. Pure Math. , 33:1–2 , Amer. Math. Soc. (1979) -functions , Proc. Symp. Pure Math. , 33:1–2 , Amer. Math. Soc. (1979) |
| [a3] | S.S. Gelbart, "Automorphic forms on adèle groups" , Princeton Univ. Press (1975) |
Automorphic form. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Automorphic_form&oldid=13843