Automata, methods of specification of
The various ways of describing automata and their functioning or behaviour. The method of specification of an automaton will depend on the approach to the concept of an automaton. If the macro-approach is adopted (cf. Automaton, finite), it is the external behaviour of an automaton which is described. If the micro-approach is adopted, the definition should include a description of the elements from which the automaton is constructed, and the schemes of their composition. Methods of specifying finite automata are described below.
Macro-approach.
To specify a finite automaton 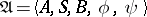 for given alphabets
for given alphabets 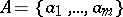 ,
, 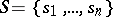 and
and 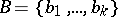 is tantamount to describing the functions
is tantamount to describing the functions 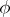 and
and 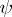 or to describing the behaviour of this automaton (cf. Automaton, behaviour of an). The functions
or to describing the behaviour of this automaton (cf. Automaton, behaviour of an). The functions 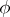 and
and  are often defined by means of a table, a diagram or a matrix of transitions. The table of transitions
are often defined by means of a table, a diagram or a matrix of transitions. The table of transitions 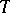 of the automaton
of the automaton 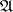 consists of two subtables
consists of two subtables 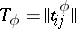 and
and 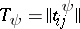 ,
, 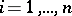 ,
, 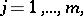
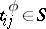 ,
, 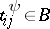 . The functions
. The functions 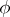 and
and 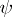 are defined by
are defined by  ,
, 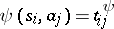 . If all the columns of
. If all the columns of 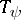 coincide, the table
coincide, the table 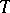 defines a Moore automaton. For instance, let
defines a Moore automaton. For instance, let 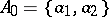 ,
,  ,
, 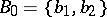 ; the table
; the table 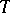 (Fig. a) will then specify the functions
(Fig. a) will then specify the functions 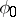 and
and 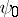 of some automaton
of some automaton 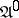 (Fig. bshows the subtables
(Fig. bshows the subtables 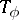 and
and 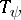 of
of 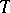 ).
).
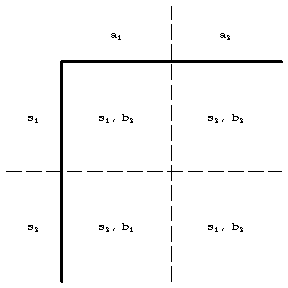
Figure: a014060a
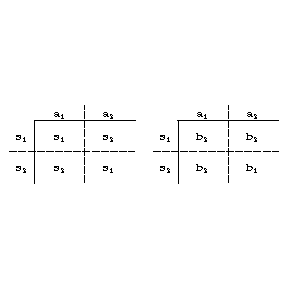
Figure: a014060b
The diagram of (transitions of) an automaton is an oriented graph 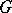 with a one-to-one correspondence between the vertices of the graph and the elements of
with a one-to-one correspondence between the vertices of the graph and the elements of 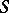 , and between the edges of the graph and certain sets of pairs of the form
, and between the edges of the graph and certain sets of pairs of the form 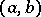 ,
, 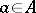 ,
, 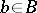 . Each vertex of
. Each vertex of  is the starting point of at least one edge, and the set
is the starting point of at least one edge, and the set 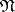 of all pairs assigned to the edges with the same vertex as their origin has the form
of all pairs assigned to the edges with the same vertex as their origin has the form 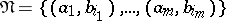 . The functions
. The functions 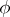 and
and 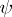 are then defined as follows:
are then defined as follows: 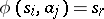 ,
, 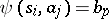 if the pair
if the pair 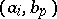 is assigned to the edge issuing from from
is assigned to the edge issuing from from 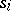 and if this edge ends in the vertex
and if this edge ends in the vertex 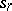 . It is convenient to formulate certain properties of automata in the language of diagrams (connectivity of an automaton, attainability of states, etc.). Fig. c shows the transition diagram of the automaton
. It is convenient to formulate certain properties of automata in the language of diagrams (connectivity of an automaton, attainability of states, etc.). Fig. c shows the transition diagram of the automaton 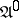 .
.
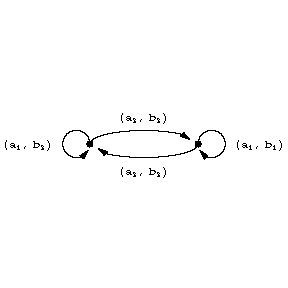
Figure: a014060c
The transition matrix is used to describe the functioning of the transition system 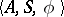 (cf.Automaton, finite). It is represented by the
(cf.Automaton, finite). It is represented by the 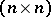 -matrix
-matrix 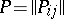 whose elements are subsets of the alphabet
whose elements are subsets of the alphabet 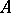 (including the empty subset) such that
(including the empty subset) such that 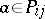 if and only if
if and only if 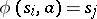 , so that for any
, so that for any 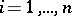 the relations
the relations 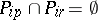 if
if 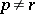 and
and 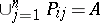 are true. In order to extend the function
are true. In order to extend the function 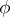 to the set
to the set 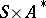 (where
(where 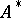 is the set of all words over the alphabet
is the set of all words over the alphabet 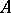 including the empty word), one considers the sequence of powers of the matrix
including the empty word), one considers the sequence of powers of the matrix 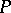 . Multiplication of
. Multiplication of 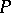 by itself is carried out by the usual algorithm, using the operations of concatenation and union of word sets instead of multiplication and addition. If
by itself is carried out by the usual algorithm, using the operations of concatenation and union of word sets instead of multiplication and addition. If 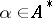 is a word of length
is a word of length 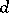 and
and 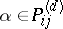 where
where 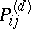 is an element of the matrix
is an element of the matrix 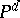 , one has
, one has 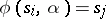 . Thus, the transition matrix
. Thus, the transition matrix 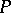 of the transition system
of the transition system 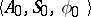 and the matrix
and the matrix 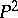 have, respectively, the forms:
have, respectively, the forms:
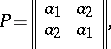 |
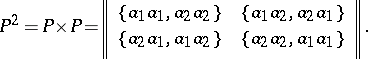 |
A number of minimization (reduction) algorithms and algorithms of automaton synthesis are associated with these methods of specifying automata.
In order to specify the behaviour of an initialized (not necessarily finite) automaton 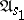 (transformer), one must define the function
(transformer), one must define the function  which maps
which maps 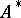 into
into 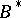 (or
(or  into
into 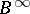 , where
, where  are the sets of all the superwords over the alphabets
are the sets of all the superwords over the alphabets  and
and  , respectively).
, respectively).
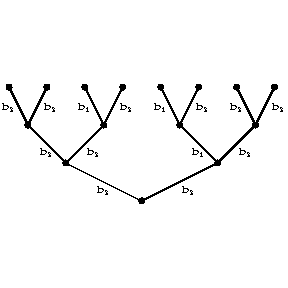
Figure: a014060d
This function may be defined by means of an information tree. From each vertex of the information tree there issue 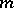 edges, which are in one-to-one correspondence with the respective letters of
edges, which are in one-to-one correspondence with the respective letters of  . To each vertex is assigned a state of the automaton
. To each vertex is assigned a state of the automaton 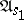 , while to each edge is assigned a letter of
, while to each edge is assigned a letter of 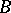 in the following way. The state
in the following way. The state 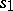 is assigned to the root. If the state
is assigned to the root. If the state 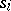 has been assigned to some vertex, the letter
has been assigned to some vertex, the letter 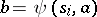 is assigned to the edge corresponding to the letter
is assigned to the edge corresponding to the letter  from
from 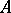 , while to the vertex in which this edge terminates the state
, while to the vertex in which this edge terminates the state 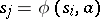 is assigned. To each word
is assigned. To each word 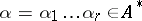 corresponds a unique sequence
corresponds a unique sequence 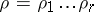 of edges of this tree such that
of edges of this tree such that 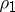 issues from the root and
issues from the root and 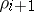 issues from the vertex of termination of
issues from the vertex of termination of  . The word
. The word 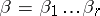 , where
, where 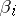 is the letter from
is the letter from 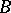 assigned to the edge
assigned to the edge 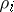 ,
, 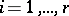 , is identical with the value
, is identical with the value 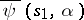 . If the function
. If the function 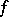 is realized by a finite automaton, the corresponding information tree may be effectively determined by means of a finite subtree. Fig. d shows the subtree of the initialized automaton
is realized by a finite automaton, the corresponding information tree may be effectively determined by means of a finite subtree. Fig. d shows the subtree of the initialized automaton 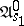 (the left-hand edges, issuing from the vertices, correspond to the symbol
(the left-hand edges, issuing from the vertices, correspond to the symbol 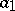 , while the right-hand edges correspond to the symbol
, while the right-hand edges correspond to the symbol 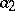 ).
).
The behaviour of a finite automaton (acceptor) in terms of a representable event (super-event) may be effected with the aid of a regular expression (cf. Regular event). Such events may also be specified as sets of words generated (derived) in some formal system (a semi-Thue grammar, etc.). In this case the semi-Thue system is given as the quadruple 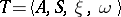 where
where 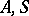 are finite alphabets,
are finite alphabets, 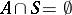 ,
,  is an axiom scheme of the form
is an axiom scheme of the form 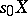 and
and 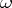 is the set of schemes of derivation rules of the form
is the set of schemes of derivation rules of the form  ,
, 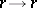 , where
, where 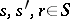 ,
, 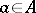 and
and 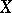 is a variable which assumes values from
is a variable which assumes values from 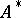 . If, moreover,
. If, moreover, 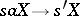 and
and 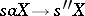 belong to
belong to 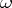 , one has
, one has 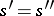 . The word
. The word 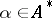 is deducible in the system
is deducible in the system 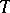 if there exists a sequence of words
if there exists a sequence of words 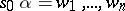 such that
such that 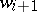 is obtained from
is obtained from 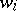 ,
, 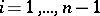 , by the application of a certain rule from
, by the application of a certain rule from 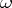 ,
, 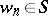 and
and 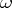 does not contain the rule
does not contain the rule 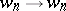 . A grammar generating a regular event has a similar form. It is given by the quadruple
. A grammar generating a regular event has a similar form. It is given by the quadruple 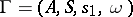 where
where 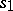 from
from 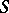 is an axiom,
is an axiom, 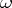 is the set of rules of the form
is the set of rules of the form 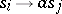 or
or 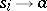 . The word
. The word 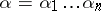 is deducible in
is deducible in 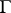 if
if 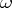 includes the rules
includes the rules  ,
, 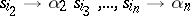 . Algorithms which yield the transition matrix of an automaton from formal schemes of this type are known. Thus, an event represented in the acceptor
. Algorithms which yield the transition matrix of an automaton from formal schemes of this type are known. Thus, an event represented in the acceptor 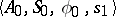 by the state
by the state 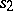 may be defined, for example, as the set of words that are deducible in the semi-Thue system
may be defined, for example, as the set of words that are deducible in the semi-Thue system
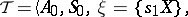 |
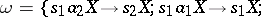 |
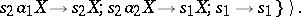 |
There exist several other ways of specifying an automaton. For instance, a (necessarily finite) transition system 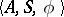 may be specified as an algebra
may be specified as an algebra 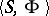 where
where 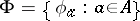 is the set of unary operations on
is the set of unary operations on 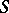 such that
such that 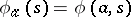 . Thus, the transition system
. Thus, the transition system 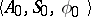 may be regarded as the algebra
may be regarded as the algebra  , where
, where 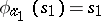 ,
, 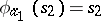 ,
,  ,
, 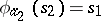 . One may also consider the algebra
. One may also consider the algebra 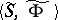 where
where 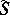 is the set of words of the form
is the set of words of the form  ,
, 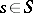 ,
, 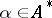 and
and 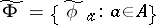 is the set of unary operations on
is the set of unary operations on 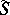 such that
such that 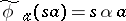 . The algebra
. The algebra 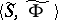 is defined by the system of
is defined by the system of 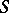 -generators and the set of defining relations
-generators and the set of defining relations 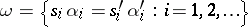 . Such an algebra specifies a (usually partial) automaton
. Such an algebra specifies a (usually partial) automaton 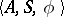 such that if
such that if 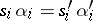 is a relation from
is a relation from  , the relation
, the relation 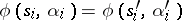 is true. For example, the transition system
is true. For example, the transition system 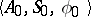 may be specified by a system of
may be specified by a system of  -generators and the set of defining relations
-generators and the set of defining relations  . It is then assumed that
. It is then assumed that 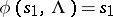 ,
, 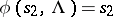 .
.
The behaviour of an automaton may be described in the language of the logic of one-place predicates. A choice of the class of formulas defining a finite automaton may be performed in various ways. The description may be incomplete, because the choice defines a class of automata whose the behaviour is identical to within the accuracy of this description. For instance, the "questionnaire" approach involves specifying classes of automata with the aid of fragments of information trees, a partial definition of the functions 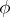 and
and  , etc.
, etc.
The above ways of specifying automata may also be applied, with suitable modifications, to the behaviour of certain generalized finite automata (non-deterministic, infinite, etc.; cf. Automaton). Thus, the elements of the table 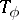 of a finite, non-deterministic automaton may consist of arbitrary subsets of the set
of a finite, non-deterministic automaton may consist of arbitrary subsets of the set 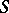 . The behaviour of a finite, non-deterministic acceptor is described by a regular expression, as in the case of a deterministic acceptor. Other generalizations of finite automata are finite probabilistic automata (cf. Automaton, probabilistic), automata over terms, mosaic structures, etc.
. The behaviour of a finite, non-deterministic acceptor is described by a regular expression, as in the case of a deterministic acceptor. Other generalizations of finite automata are finite probabilistic automata (cf. Automaton, probabilistic), automata over terms, mosaic structures, etc.
To specify a probabilistic automaton 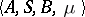 on known alphabets
on known alphabets 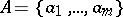 ,
, 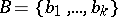 ,
, 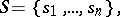 means to specify, for any given
means to specify, for any given 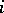 and
and 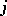 (
(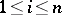 ,
,  ) an arbitrary probability measure
) an arbitrary probability measure  on the set of all pairs
on the set of all pairs 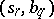 ,
,  ,
, 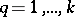 . To do this, one usually considers a system of square matrices with non-negative elements
. To do this, one usually considers a system of square matrices with non-negative elements
 |
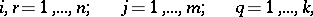 |
such that each matrix 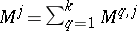 is stochastic. The measure
is stochastic. The measure 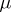 is defined by the relation
is defined by the relation 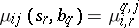 . The probabilistic automaton
. The probabilistic automaton 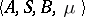 is considered in conjunction with a certain initial probability distribution on the set
is considered in conjunction with a certain initial probability distribution on the set 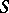 :
:
 |
Sometimes probabilistic automata are defined by specifying only the matrices 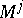 or only the matrices
or only the matrices  , where
, where
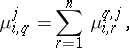 |
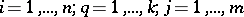 . Any finite Markov chain can be regarded as a finite probabilistic automaton in which the matrices
. Any finite Markov chain can be regarded as a finite probabilistic automaton in which the matrices 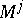 ,
,  , are identical. The system of matrices shown below defines some probabilistic automaton
, are identical. The system of matrices shown below defines some probabilistic automaton 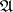 (
(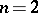 ,
,  ,
, 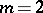 ) and the matrices
) and the matrices 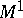 ,
, 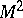 ,
, 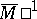 ,
, 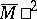 of this automaton:
of this automaton:
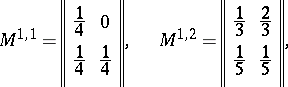 |
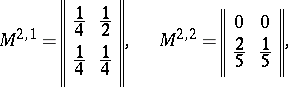 |
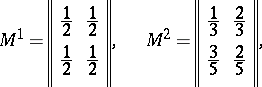 |
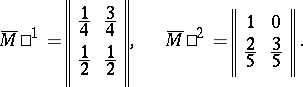 |
In order to define a finite automaton over terms  when the alphabets
when the alphabets 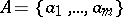 and
and 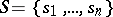 are known one must first specify a mapping
are known one must first specify a mapping 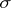 of the set
of the set 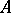 into the finite set of non-negative integers such that there exists at least one element
into the finite set of non-negative integers such that there exists at least one element 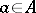 for which
for which 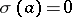 and, secondly, one must define, for each
and, secondly, one must define, for each 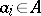 ,
, 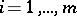 , a
, a 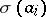 -ary function
-ary function 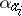 mapping the set
mapping the set 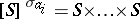 into
into 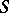 . To each element
. To each element  for which
for which 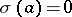 there corresponds an element
there corresponds an element 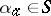 , called an initial state of the automaton. For example, if
, called an initial state of the automaton. For example, if  ,
, 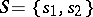 ,
, 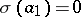 ,
, 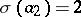 ,
,  ,
, 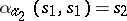 ,
, 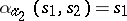 ,
, 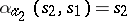 ,
,  , then the functions
, then the functions 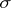 ,
,  ,
, 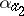 define some automaton over terms
define some automaton over terms 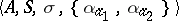 with initial state
with initial state 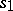 .
.
In order to specify a mosaic structure (an infinite union of transition systems of the form 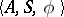 , where
, where 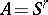 , cf. Automaton), one must define for each integral point of the
, cf. Automaton), one must define for each integral point of the  -dimensional space an ordered set of integral points; this set is called its neighbourhood. The input alphabet
-dimensional space an ordered set of integral points; this set is called its neighbourhood. The input alphabet  of the transition system
of the transition system 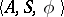 placed at a given point is the Cartesian product of the set of states of the transition systems placed at the points of its neighbourhood. For example, let
placed at a given point is the Cartesian product of the set of states of the transition systems placed at the points of its neighbourhood. For example, let 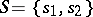 , and let the ordered set
, and let the ordered set 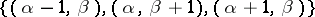 be the neighbourhood
be the neighbourhood 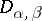 of an integral point
of an integral point 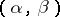 of the two-dimensional space. In order to specify a uniform two-dimensional mosaic structure, the function
of the two-dimensional space. In order to specify a uniform two-dimensional mosaic structure, the function 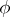 is defined as follows:
is defined as follows: 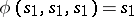 ; in all other cases
; in all other cases 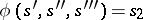 . Here, the input alphabet
. Here, the input alphabet 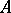 is the Cartesian product
is the Cartesian product 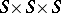 .
.
Micro-approach.
A micro-approach definition of a structural automaton describes its constituent elements and the scheme of their combination. This description may be detailed or more general. It is frequently restricted to the so-called canonical scheme of the construction of an automaton. The elements then divide into two groups: functional elements (one-state automata) and memory elements. The canonical scheme (Fig. e) consists of two functional blocks 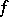 and
and  to which are added Moore automata
to which are added Moore automata 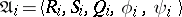 ,
, 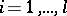 , as memory elements. The blocks
, as memory elements. The blocks  and
and 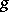 consist of functional elements. When the structure is defined in this way, these blocks are not further described, but a specification is given (e.g. by means of tables) of the vector functions realized by these blocks:
consist of functional elements. When the structure is defined in this way, these blocks are not further described, but a specification is given (e.g. by means of tables) of the vector functions realized by these blocks:
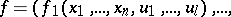 |
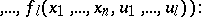 |
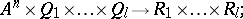 |
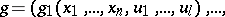 |
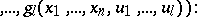 |
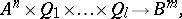 |
where 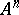 and
and 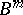 are the input and the output alphabets, respectively, of the canonical scheme.
are the input and the output alphabets, respectively, of the canonical scheme.
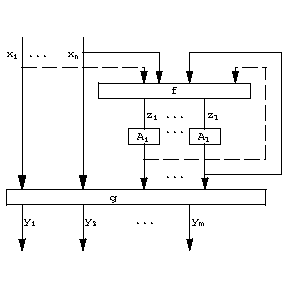
Figure: a014060e
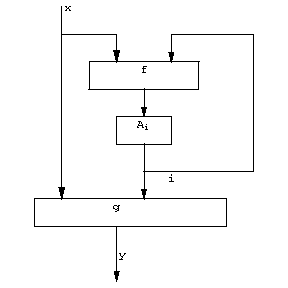
Figure: a014060f
This scheme specifies the structural automaton 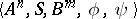 , where
, where 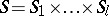 , while the functions
, while the functions 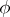 and
and 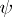 are defined as follows:
are defined as follows:
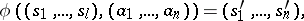 |
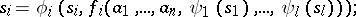 |
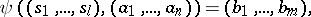 |
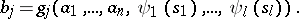 |
An important example of structural automata are logical networks (cf. Automaton, finite). Fig. f shows the canonical scheme of an automaton 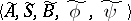 isomorphic to the automaton
isomorphic to the automaton 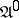 (cf. Fig. cfor its diagram),
(cf. Fig. cfor its diagram),  . The automaton
. The automaton 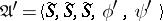 is a Moore automaton such that
is a Moore automaton such that 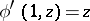 ,
, 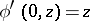 .
.
Structural automata are frequently described by means of canonical equations, i.e. systems of the form
 |
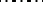 |
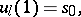 |
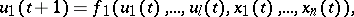 |
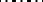 |
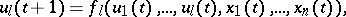 |
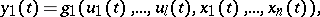 |
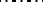 |
 |
where 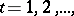 is an integer parameter,
is an integer parameter, 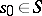 , while the functions
, while the functions  ,
, 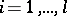 ,
, 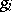 ,
, 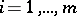 , and the variables
, and the variables 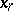 ,
, 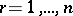 , take their values from the set
, take their values from the set 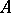 . A canonical scheme in which all the memory elements are identical corresponds to this system:
. A canonical scheme in which all the memory elements are identical corresponds to this system: 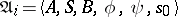 , where
, where 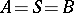 ,
, 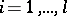 ;
; 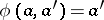 ,
, 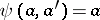 . The functioning of the automaton
. The functioning of the automaton 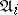 may essentially be described as follows. At the moment
may essentially be described as follows. At the moment 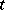 suppose that the letter
suppose that the letter 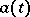 is assigned to the input of
is assigned to the input of 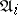 , then the same letter is produced as the output of
, then the same letter is produced as the output of 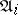 at the moment
at the moment 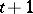 . Let Fig. f represent an automaton
. Let Fig. f represent an automaton 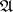 whose canonical equations have the form
whose canonical equations have the form
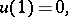 |
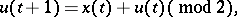 |
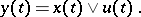 |
In the general case, a description of structural automata involves defining a selection of elementary automata and a certain class of "correctly constructed" schemes (networks), the latter usually being defined by induction.
References
| [1] | C.E. Shannon (ed.) J. McCarthy (ed.) , Automata studies , Princeton Univ. Press (1956) |
| [2] | V.M. Glushkov, "Synthesis of numerical automata" , Moscow (1962) (In Russian) |
Comments
See the Editorial Comment to the article Automata, equivalence of.
Automata, methods of specification of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Automata,_methods_of_specification_of&oldid=11434