Automata, equivalence of
An equivalence relation on the set of automata, which arises in the context of studying some individual internal properties of automata. Such a property is usually the behaviour of automata (cf. Automaton, behaviour of an), since two automata are considered equivalent if their behaviour is identical. In this context the behaviour of an automaton is usually understood to be the totality of functions realized by it (cf. Automaton, finite). For finite automata such an equivalence relation is solvable, and for this reason there exists a minimization algorithm for automata, i.e. an algorithm used to construct for a given automaton an equivalent automaton with the smallest possible number of states (a minimal automaton).
Equivalence of automata is conveniently defined in terms of the concept of equivalence of states: Two states  and
and 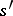 of the automata
of the automata  and
and 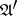 (they may be identical) are said to be equivalent if the initialized automata
(they may be identical) are said to be equivalent if the initialized automata  and
and 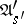 realize the same function. Such an equivalence of the automata
realize the same function. Such an equivalence of the automata 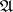 and
and  will then mean that it is possible to find, for an arbitrary state of
will then mean that it is possible to find, for an arbitrary state of 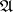 , a state of
, a state of 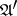 equivalent to it, and vice versa. An automaton is minimal if and only if no two states of it are equivalent. The minimal automaton is unambiguously defined for any automaton, up to an isomorphism. The algorithm of solution of this equivalence relation for finite automata is based on Moore's theorem, according to which states
equivalent to it, and vice versa. An automaton is minimal if and only if no two states of it are equivalent. The minimal automaton is unambiguously defined for any automaton, up to an isomorphism. The algorithm of solution of this equivalence relation for finite automata is based on Moore's theorem, according to which states  and
and 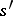 of
of 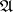 are equivalent precisely if the functions realized by the initialized automata
are equivalent precisely if the functions realized by the initialized automata 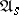 and
and 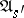 are identical on words of length
are identical on words of length 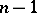 , where
, where  is the number of states of
is the number of states of  . If the states
. If the states  and
and 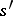 belong, respectively, to two automata
belong, respectively, to two automata 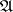 and
and  , the estimate is equal to
, the estimate is equal to  , where
, where  is the number of states of
is the number of states of 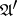 . This theorem also forms the principle of a well-known minimization algorithm of finite automata, which involves the construction of the so-called reduced automaton, the states of which are classes of equivalent states, while its transition and output functions are naturally induced by the corresponding functions of the original automaton. A reduced automaton is minimal, since any two of its states are non-equivalent.
. This theorem also forms the principle of a well-known minimization algorithm of finite automata, which involves the construction of the so-called reduced automaton, the states of which are classes of equivalent states, while its transition and output functions are naturally induced by the corresponding functions of the original automaton. A reduced automaton is minimal, since any two of its states are non-equivalent.
There exist asymptotic estimates of the number  of minimal automata with
of minimal automata with  states,
states, 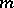 input and
input and  output letters; if
output letters; if 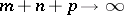 for
for  , the estimate is
, the estimate is 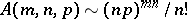 , while
, while
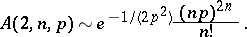 |
Another problem in the study of equivalence of automata is the problem of equivalent transformations of automata. This problem was studied for two of the possible ways of defining finite automata — diagrams and logical networks. Generally speaking, the problem consists in finding a system of transformation rules which satisfy certain conditions and which enable one to transform any given automaton into an automaton equivalent to it: a so-called complete system of rules. In both cases the transformation rule is a pair of schemes (fragments of diagrams or logical networks) which realize identical choices of mappings. The rule is applied by substituting one fragment for another. For finite automata a complete system of rules cannot exist, but they do exist for logical networks with a limited number of delays.
The fundamental concepts, problems and methods which arise in the study of the equivalence of finite automata are usually extended to other types of automata, with due regard for their particular features. For references see Automaton.
Comments
The reader is referred to the articles Formal languages and automata and  -systems. Most of the topics in this article are nowadays not considered to be in the mainstream anymore.
-systems. Most of the topics in this article are nowadays not considered to be in the mainstream anymore.
Automata, equivalence of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Automata,_equivalence_of&oldid=16236