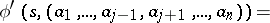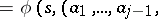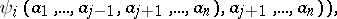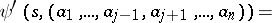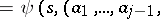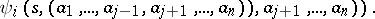Operations by which more complex automata are obtained from other automata by combining the initial automata in accordance with certain rules. Composition of automata plays an important role in problems of synthesis and decomposition of automata. The most important and the most frequently used compositions of automata are the direct product, superposition and feedback.
The direct product of automata 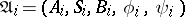 ,
,  , is the automaton
, is the automaton  for which
for which
while the functions  and
and  are defined by the relations
are defined by the relations
The superposition of automata 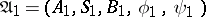 and
and 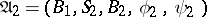 is the automaton
is the automaton 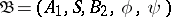 for which
for which 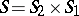 and
and
where 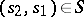 and
and 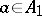 .
.
In problems of completeness and synthesis of automata the feedback operation is very important. This operation is applicable to automata with  inputs and
inputs and 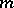 outputs
outputs  where
where 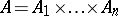 ,
,  ,
,
such that for certain 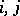 the relation
the relation 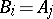 is true and the function
is true and the function 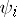 is independent of
is independent of  , i.e.
, i.e.
Under these conditions, the feedback operation on the 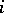 -th output and
-th output and  -th input of automaton
-th input of automaton 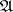 yields the automaton
yields the automaton 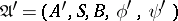 such that
such that 
There are also other kinds of compositions of automata, e.g. the product, direct sum, semi-direct product, etc.
References
| [1] | V.M. Glushkov, "The abstract theory of automata" Russian Math. Surveys , 16 : 5 (1961) pp. 1–53 Uspekhi Mat. Nauk , 16 : 5 (1961) pp. 3–62 |
| [2] | V.B. Kudryavtsev, "On the cardinality of sets of pre-complete sets of certain function systems, related to automata" Problemy Kibernet. (1965) pp. 45–74 (In Russian) |
For more information see [a1].
References
| [a1] | F. Géiseg, "Products of automata" , Springer (1986) |
How to Cite This Entry:
Automata, composition of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Automata,_composition_of&oldid=15462
This article was adapted from an original article by V.N. Red'ko (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article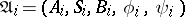 ,
,  , is the automaton
, is the automaton  for which
for which

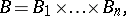
 and
and  are defined by the relations
are defined by the relations
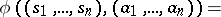

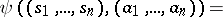
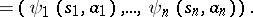
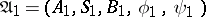 and
and 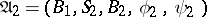 is the automaton
is the automaton 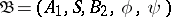 for which
for which 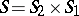 and
and
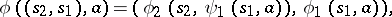
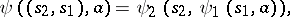
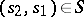 and
and 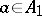 .
.
 inputs and
inputs and 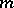 outputs
outputs  where
where 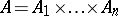 ,
,  ,
,
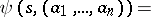
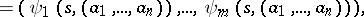
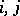 the relation
the relation 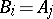 is true and the function
is true and the function 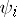 is independent of
is independent of  , i.e.
, i.e.
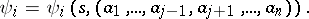
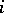 -th output and
-th output and  -th input of automaton
-th input of automaton 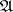 yields the automaton
yields the automaton 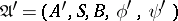 such that
such that