Attainable boundary point
A point on the boundary of a domain together with the class of equivalent paths leading from the interior of the domain to that point. Let  be a point on the boundary
be a point on the boundary  of a domain
of a domain  in the complex
in the complex  -plane and let there exist a path described by the equation
-plane and let there exist a path described by the equation  , where the function
, where the function  is defined and continuous on a certain segment
is defined and continuous on a certain segment  ,
,  if
if  ,
,  . One then says that this path leads to the point
. One then says that this path leads to the point 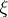 (from the inside of
(from the inside of 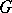 ) and defines the attainable boundary point represented by
) and defines the attainable boundary point represented by  . Two paths leading to
. Two paths leading to 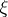 are said to be equivalent (or, defining the same attainable boundary point) if there exists a third path which also leads to
are said to be equivalent (or, defining the same attainable boundary point) if there exists a third path which also leads to  from the inside of
from the inside of 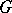 and which has non-empty intersections inside
and which has non-empty intersections inside 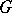 as close to
as close to 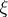 as one pleases with each of the two paths considered. The totality of a point
as one pleases with each of the two paths considered. The totality of a point 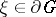 and the class of equivalent paths leading to
and the class of equivalent paths leading to 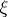 from the interior of
from the interior of 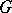 is said to be an attainable boundary point of the domain
is said to be an attainable boundary point of the domain  . Not every point
. Not every point 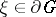 represents an attainable boundary point; on the other hand, the same point
represents an attainable boundary point; on the other hand, the same point 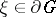 can represent several, or even an infinite set of different, attainable boundary points.
can represent several, or even an infinite set of different, attainable boundary points.
An attainable boundary point is the unique point of a prime end (cf. Limit elements) of the first kind; a (multi-point) prime end of the second kind contains exactly one attainable boundary point, while prime ends of the third and fourth kinds do not contain attainable boundary points. Each point of the boundary of a Jordan domain is attainable.
References
| [1] | A.I. Markushevich, "Theory of functions of a complex variable" , 3 , Chelsea (1977) (Translated from Russian) |
| [2] | E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 1;6 |
Comments
The standard Western terminology is accessible boundary point.
Attainable boundary point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Attainable_boundary_point&oldid=14913