Asymptotic value
A limit value along some path. More exactly, a complex number 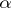 or
or  is called an asymptotic value for a function
is called an asymptotic value for a function 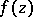 of the complex variable
of the complex variable  at a point
at a point  of the closure
of the closure  of its domain of definition
of its domain of definition  if there exists a path
if there exists a path 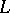 :
: 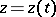 ,
, 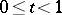 ,
, 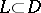 , terminating at
, terminating at  , i.e. so that
, i.e. so that
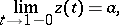 |
along which
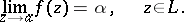 |
For instance, at the point  the function
the function  has the asymptotic values
has the asymptotic values  and
and  along the paths
along the paths 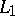 :
:  ,
, 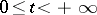 , and
, and 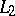 :
:  ,
,  , respectively. Sets of asymptotic values play an important role in the theory of limit sets (cf. Limit set).
, respectively. Sets of asymptotic values play an important role in the theory of limit sets (cf. Limit set).
If  has two different asymptotic values at
has two different asymptotic values at  ,
,  is called a point of indeterminacy for the function
is called a point of indeterminacy for the function 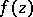 . For any function
. For any function 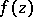 , defined in a simply-connected plane domain, the set of points of indeterminacy is at most countable.
, defined in a simply-connected plane domain, the set of points of indeterminacy is at most countable.
The above definition of asymptotic value refers to asymptotic point values. If the limit set of a curve  is a set
is a set 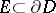 rather than a single point
rather than a single point  , one also speaks of the asymptotic value
, one also speaks of the asymptotic value 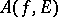 associated with
associated with 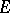 .
.
References
| [1] | E.F. Collingwood, A.J. Lohwater, "The theory of cluster sets" , Cambridge Univ. Press (1966) pp. Chapt. 1;6 |
| [2] | G.R. MacLane, "Asymptotic values of holomorphic functions" , Rice Univ. Studies, Math. Monographs , 49 : 1 , Rice Univ. , Houston (1963) |
Comments
The most famous results on asymptotic values is the Denjoy–Carleman–Ahlfors theorem. Let 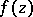 be an entire function with
be an entire function with  distinct (finite) asymptotic values at the point
distinct (finite) asymptotic values at the point 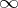 . Then
. Then 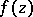 must be of order
must be of order 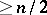 . This result was conjectured by A. Denjoy (1907). The first complete proof was given by L. Ahlfors (1929), after T. Carleman had obtained a less sharp result. See, for example, [a1], Sect. 60.
. This result was conjectured by A. Denjoy (1907). The first complete proof was given by L. Ahlfors (1929), after T. Carleman had obtained a less sharp result. See, for example, [a1], Sect. 60.
References
| [a1] | A. Dinghas, "Vorlesungen über Funktionentheorie" , Springer (1961) |
Asymptotic value. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Asymptotic_value&oldid=18288