Asymptotic negligibility
A property of random variables indicating that their individual contribution as components of a sum is small. This concept is important, for example, in the so-called triangular array. Let the random variables  (
( ;
;  ) be mutually independent for each
) be mutually independent for each  , and let
, and let
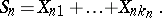 |
If for all  and
and  , at sufficiently large values of
, at sufficiently large values of  , the inequality
, the inequality
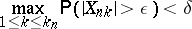 | (1) |
is satisfied, the individual terms 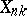 are called asymptotically negligible (the variables
are called asymptotically negligible (the variables  then form a so-called zero triangular array). If condition (1) is met, one obtains the following important result: The class of limit distributions for
then form a so-called zero triangular array). If condition (1) is met, one obtains the following important result: The class of limit distributions for  (
(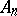 are certain "centering" constants) coincides with the class of infinitely-divisible distributions (cf. Infinitely-divisible distribution). If the distributions of
are certain "centering" constants) coincides with the class of infinitely-divisible distributions (cf. Infinitely-divisible distribution). If the distributions of 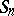 converge to a limit distribution,
converge to a limit distribution, 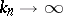 , and the terms are identically distributed, condition (1) is automatically met. If the requirement for asymptotic negligibility is strengthened by assuming that for all
, and the terms are identically distributed, condition (1) is automatically met. If the requirement for asymptotic negligibility is strengthened by assuming that for all 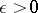 and
and  for all sufficiently large
for all sufficiently large  one has
one has
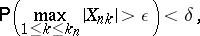 | (2) |
then the following statement is valid: If (2) is met, the limit distribution for 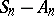 can only be a normal distribution (in particular with variance equal to zero, i.e. a degenerate distribution).
can only be a normal distribution (in particular with variance equal to zero, i.e. a degenerate distribution).
Comments
References
| [a1] | W. Feller, "An introduction to probability theory and its applications" , 2 , Wiley (1966) pp. 210 |
Asymptotic negligibility. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Asymptotic_negligibility&oldid=13553