Asymptotic equality
Two functions  and
and  are called asymptotically equal as
are called asymptotically equal as  if in some neighbourhood of the point
if in some neighbourhood of the point  (except possibly at
(except possibly at  itself)
itself)
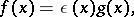 |
where
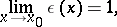 |
i.e.
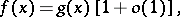 |
as  (
( is a finite or an infinite point of the set on which the functions under consideration are defined). If
is a finite or an infinite point of the set on which the functions under consideration are defined). If  does not vanish in some neighbourhood of
does not vanish in some neighbourhood of 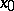 , this condition is equivalent to the requirement
, this condition is equivalent to the requirement
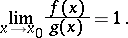 |
In other words, asymptotic equality of two functions 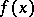 and
and 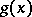 as
as  means, in this case, that the relative error of the approximate equality of
means, in this case, that the relative error of the approximate equality of 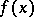 and
and  , i.e. the magnitude
, i.e. the magnitude 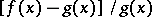 ,
, 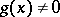 , is infinitely small as
, is infinitely small as  . Asymptotic equality of functions is meaningful for infinitely-small and infinitely-large functions. Asymptotic equality of two functions
. Asymptotic equality of functions is meaningful for infinitely-small and infinitely-large functions. Asymptotic equality of two functions 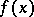 and
and 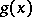 is denoted by
is denoted by 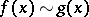 as
as 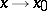 , and is reflexive, symmetric and transitive. Accordingly, the set of infinitely-small (infinitely-large) functions as
, and is reflexive, symmetric and transitive. Accordingly, the set of infinitely-small (infinitely-large) functions as 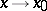 is decomposed into equivalence classes of such functions. An example of asymptotically-equal functions (which are also called equivalent functions) as
is decomposed into equivalence classes of such functions. An example of asymptotically-equal functions (which are also called equivalent functions) as 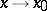 are the functions
are the functions 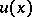 ,
, 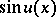 ,
, 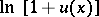 ,
, 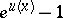 , where
, where  .
.
If  and
and 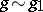 as
as 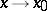 , then
, then
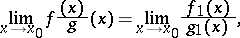 |
where the existence of any one of the limits follows from the existence of the other one. See also Asymptotic expansion of a function; Asymptotic formula.
Comments
One also says that 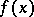 and
and 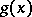 are of the same order of magnitude at
are of the same order of magnitude at 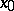 instead of asymptotically equal.
instead of asymptotically equal.
References
| [a1] | R. Courant, "Differential and integral calculus" , 1 , Blackie (1948) pp. Chapt. 3, Sect. 9 (Translated from German) |
Asymptotic equality. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Asymptotic_equality&oldid=18135