Asymptotic direction
A direction on a regular surface in which the curvature of the normal section of the surface is zero. For the direction 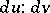 at a point
at a point 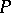 to be an asymptotic direction, the following condition is necessary and sufficient:
to be an asymptotic direction, the following condition is necessary and sufficient:
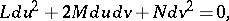 |
where  and
and  are interior coordinates on the surface, while
are interior coordinates on the surface, while 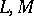 and
and 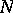 are the coefficients of the second fundamental form of the surface, calculated at
are the coefficients of the second fundamental form of the surface, calculated at 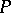 . At an elliptic point of the surface the asymptotic directions are imaginary, at a hyperbolic point there are two real asymptotic directions, at a parabolic point there is one real asymptotic direction, and at a flat point any direction is asymptotic. Asymptotic directions are self-conjugate directions (cf. Conjugate directions).
. At an elliptic point of the surface the asymptotic directions are imaginary, at a hyperbolic point there are two real asymptotic directions, at a parabolic point there is one real asymptotic direction, and at a flat point any direction is asymptotic. Asymptotic directions are self-conjugate directions (cf. Conjugate directions).
References
| [1] | P.K. Rashevskii, "A course of differential geometry" , Moscow (1956) (In Russian) |
Comments
References
| [a1] | C.C. Hsiung, "A first course in differential geometry" , Wiley (1981) |
| [a2] | D.J. Struik, "Lectures on classical differential geometry" , Addison-Wesley (1950) |
Asymptotic direction. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Asymptotic_direction&oldid=13826