Asymptote

of a curve with an infinite branch

A straight line the distance of which from the point 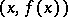on the curve tends to zero as the point moves along the branch of the curve to infinity. An asymptote can be vertical or inclined. The equation of a vertical asymptote is , where () as (from one side) is satisfied. An inclined asymptote, with equation , exists if and only if the limits

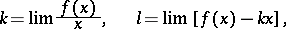exist as (or as ).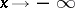

Similar formulas are also obtained for parametrized (unbounded) curves in general parametric representation. In polar coordinates an asymptote of a curve 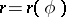, where 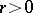, with slope angle 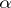, is defined by the condition as 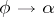. The distance 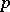of this asymptote from the coordinate origin is calculated by the formula

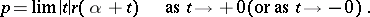If there exists a limit position of the tangent line to the infinite branch of the curve, this position is an asymptote. The converse is not always true. Thus, the curve 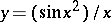has the asymptote 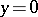as 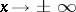, even though a limit position of the tangent line does not exist. Hyperbolas are the only second-order curves with asymptotes. The asymptotes of the hyperbola 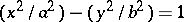are given by the equations 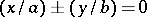. An inclined asymptote yields a simple (linear with respect to ) asymptotic approximation of the function:

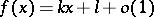as (or as ).

References

[1]	P.K. Rashevskii, "A course of differential geometry" , Moscow (1956) (In Russian)
[2]	L.D. Kudryavtsev, "Mathematical analysis" , Moscow (1973) (In Russian)

References

[a1]	A.V. Pogorelov, "Differential geometry" , Noordhoff (1959) (Translated from Russian)