Astrophysics, mathematical problems of
A type of problems in theoretical astrophysics in which mathematical methods of investigation are extensively employed. The principal task of theoretical astrophysics is the interpretation of results of observations with the purpose of studying the structure of the objects encountered in the Universe, and to study the physical processes taking place in it. In addition, there are certain mathematical problems of a general nature which are important not only in astrophysics, but also in other branches of physics and in mathematics. The most obvious example of the influence of mathematical problems in astrophysics on the development of mathematics is the so-called principle of invariance (cf. Invariance, principle of) [1], which was first considered in astrophysics, after which it was used to solve a wide class of problems in mathematical physics and certain problems in probability theory.
One of the principal problems in astrophysics is the study of the structure and the evolution of stars, since the bulk of the matter present in the Universe is concentrated in the stars. It is common to deal with the internal structure of the stars separate from the structure of stellar atmospheres. The problems in the theory of the internal structure are formulated as differential equations, resulting from the conditions of mechanical and energetic equilibrium of the star [2]. The condition of mechanical equilibrium of a star is expressed as the equality of the force of attraction directed towards the interior of the star and the force of the pressure exerted by the gases and by light, which is directed outwards. The condition of energetic equilibrium is an expression of the equality of the amount of energy produced in a given volume of the star and the amount of energy emitted by this volume. In addition to the equilibrium conditions, the equations of state of the stellar matter, the absorption coefficient of the radiation and the law of emission of energy as a result of thermonuclear reactions, as a function of the density of the matter and of the temperature for the given chemical composition, are assumed to be known. Owing to the complexity of the equations, they are usually solved by numerical methods. The results of the theory of stellar atmospheres are sometimes employed as the boundary conditions, which renders the conclusions more reliable. These equations of stellar equilibrium may be reduced in a significant number of cases to the Emden equation:
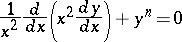 | (1) |
with the conditions 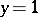 and
and 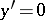 when
when 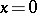 . If
. If  assumes one of the values
assumes one of the values 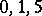 , the solutions of equation (1) may be expressed by elementary functions. Equation (1) is applicable, for example, in the zones of the star in which the energy transfer mainly takes place by a convective flow, while the transfer of radiation energy is relatively small. Another difficulty in developing the theory of the internal structure of stars is that the interiors of stars cannot be observed. Observational data are usually compared only with the calculated integral characteristics of the star such as its mass, its radius and the integral amount of energy emitted by the star in unit time. The use of statistical material concerning these characteristics makes it possible to present hypotheses on the possible evolution of stars.
, the solutions of equation (1) may be expressed by elementary functions. Equation (1) is applicable, for example, in the zones of the star in which the energy transfer mainly takes place by a convective flow, while the transfer of radiation energy is relatively small. Another difficulty in developing the theory of the internal structure of stars is that the interiors of stars cannot be observed. Observational data are usually compared only with the calculated integral characteristics of the star such as its mass, its radius and the integral amount of energy emitted by the star in unit time. The use of statistical material concerning these characteristics makes it possible to present hypotheses on the possible evolution of stars.
The theory of stellar atmospheres is based on the studies of processes of radiative transfer (cf. Radiative transfer theory). The energy generated in the interior of the star undergoes a complex process of transfer through the atmosphere, after which it emerges to the outside. The transfer equation is solved in this case under conditions of radiation equilibrium, which expresses the fact that each volume element of the atmosphere radiates and absorbs equal amounts of energy. The presence of a local thermodynamic equilibrium is also frequently postulated. In theory, the solution of the transfer equation under the above conditions yields the spectrum of the star, the comparison of which with the results of observations provides information on the structure of the stellar atmosphere and on the processes taking place in it. In particular, the determination of the chemical composition of stellar atmospheres is based on the study of the line spectra of the star.
Radiative transfer processes also take place in nebulae and in the interstellar space. The transfer process often consists in repeated light scattering as it passes through matter. Sunlight, after being dispersed in the planetary atmosphere, provides information about its structure and its physical properties. Anisotropic light scattering takes place in atmospheres of planets and in dusty nebulae.
The theory of radiative transfer is one of the most important branches of theoretical astrophysics. This theory owes its impressive development [3], [4] to the solution of the astrophysical problems mentioned above. Its methods are also extensively employed in other branches of physics such as geophysics (cf. Geophysics, mathematical problems in), in the theory of neutron transfer and in the calculations of the luminescence of plasmas. Most frequently, radiation takes place through a plane layer of matter. An example of this are stellar and planetary atmospheres, since their thickness is usually small in comparison to their radius. In this case, for isotropic scattering, the radiative transfer equation is reduced to the integral equation
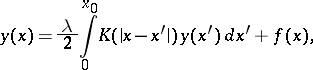 | (2) |
where 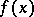 defines the distribution of the radiation sources in the layer, while
defines the distribution of the radiation sources in the layer, while 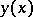 is the unknown radiation field. The kernel
is the unknown radiation field. The kernel 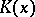 of the integral equation and the parameter
of the integral equation and the parameter 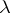 include the law of interaction of radiation with matter, while
include the law of interaction of radiation with matter, while 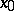 is the thickness of the layer, expressed in unit lengths of the free path of radiation. The study of integral equations of the type (2) is one of the principal mathematical problems of radiation theory. The mathematical problems of astrophysics include the search for exact analytic solutions of such equations [4]. In particular, if
is the thickness of the layer, expressed in unit lengths of the free path of radiation. The study of integral equations of the type (2) is one of the principal mathematical problems of radiation theory. The mathematical problems of astrophysics include the search for exact analytic solutions of such equations [4]. In particular, if 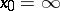 ,
, 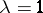 and
and 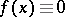 , as well as
, as well as 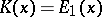 , where
, where 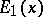 is the first integral exponential function, equation (2) is known as Milne's equation. Its solution (cf. Milne problem) under the assumption of certain supplementary conditions yields the distribution of the temperature in the interior of the stars. In more complicated problems (anisotropic scattering, scattering of polarized light, light scattering in a medium of arbitrary shape, etc.) the resulting unknown function is not the function
is the first integral exponential function, equation (2) is known as Milne's equation. Its solution (cf. Milne problem) under the assumption of certain supplementary conditions yields the distribution of the temperature in the interior of the stars. In more complicated problems (anisotropic scattering, scattering of polarized light, light scattering in a medium of arbitrary shape, etc.) the resulting unknown function is not the function 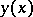 , but functions which depend not only on the coordinates but also on the direction and on other magnitudes which characterize the radiation field at the given point. These functions are determined with the aid of appropriate systems of integral equations, which are a generalization of (2).
, but functions which depend not only on the coordinates but also on the direction and on other magnitudes which characterize the radiation field at the given point. These functions are determined with the aid of appropriate systems of integral equations, which are a generalization of (2).
These methods are used to find the complete solution of the problem, which makes it possible to find both the radiation field inside the medium and the characteristics of the radiation emitted by the medium. In the applications of the theory it is often only necessary to know the emitted radiation. It has been shown that it is possible to determine the characteristics of the radiation emitted by the medium directly, without previously finding the complete solution. This often simplifies the task considerably, and is realized either by using the integral equation (2) or by applying the principle of invariance. The other approach consists in representing the given layer as a sum of two layers and establishing the relations between the characteristics of the radiation emitted by the medium as a whole and the radiation characteristics at the boundaries of the two layers. These techniques are also applied in the theory of neutron transfer, where they are known as the Albedo method.
Another prominent subject in astrophysics is the application of methods of gas dynamics [5] and electrodynamics [6] to the study of stars and interstellar space. These methods are indispensable in the study of the motion of gas masses in stars and nebulae. The hydrodynamic effects (cf. Hydrodynamics, mathematical problems in) in the atmospheres of the Sun and other stars, the expansion of gas clouds and their collisions with each other and with the more rarefied interstellar medium, as well as resulting shock waves and turbulent motions in it are some of the problems studied.
One of the more important features of interstellar gas dynamics is the necessity of considering the interaction of an ionized gas with magnetic fields. This interaction affects both the motion of the gas and the changes in the configuration and the energy density of the magnetic field. When the gas is in motion, its particles "adhere" all the time, as it were, to the magnetic line of force, moving along it or dragging it with them as they move across the field. One says that that the lines of force are "frozen" into the matter (cf. Frozen-in integral). The equations of motion of interstellar magnetic gas dynamics include: the continuity equation (the law of conservation of mass); the induction equation of the magnetic field, which expresses the frozen-in principle; the equation of the influx of the energy of interstellar radiation (the law of conservation of energy); and the equation which expresses the law of conservation of momentum. The system is established using the electrodynamic equations (Maxwell equations) and the hydrodynamic equations. The solution of this system is highly complicated, since the equations are non-linear. There usually exist simplified variants, e.g. one-dimensional and auto-modelling motions (cf. Magneto-hydrodynamics, mathematical problems in).
Results obtained by radio-astronomic methods are highly important in the development of astrophysics. Since the radiation of radio waves usually takes place in an ionized gas (a plasma), there arise the problems of determining the properties of the plasma under the conditions that exist in stars and in interstellar space [7]. The behaviour of the plasma can be most fully described by means of a kinetic equation. The difference between the kinetic equation for a plasma and the kinetic Boltzmann equation for an ordinary gas consists in the fact that the Coulomb interaction of the charged particles of the plasma extends to relatively large distances, while in a gas consisting of neutral atoms and molecules, the interactions are significant only during direct collisions.
The study of the distribution of matter in the Galaxy is made more difficult by the absorption of light by the interstellar dust particles. This effect is particularly marked in directions close to the Milky Way, since the layer of interstellar dust is concentrated near the plane of the Galaxy. This effect of light absorption is also responsible for the decrease in the number of observed galaxies as the direction of viewing approaches the plane of our Galaxy. However, the absorbing substance is not uniformly distributed; rather, it forms discrete clouds of differing magnitudes, randomly distributed in space. Thus there arises the problem of the statistical study of the apparent distribution of the brightness of the Milky Way and of the apparent distribution of galaxies. These problems were studied in detail [1] in the theory of fluctuations in brightness of the Milky Way. The relevant equations were derived using the principle of invariance. The mathematical problems of the theory of the fluctuation of brightness are close to the theory of certain types of random processes. In their simplest variant it is assumed that the entire equatorial plane of the galaxy is infinitely filled, at a uniform density, with stars and with light-absorbing clouds. If it is assumed that the proportion of the transmitted light 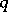 is the same for all clouds, and that
is the same for all clouds, and that 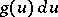 is the probability of the dimensionless brightness being included between
is the probability of the dimensionless brightness being included between  and
and 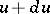 , the function
, the function 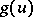 will be given by the equation
will be given by the equation
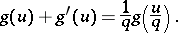 | (3) |
Equations of a similar type result on considering more general models as well. The results of the observations are frequently interpreted by using moments of the magnitudes under study; accordingly, the solution of the complicated initial equations is not invariably necessary. The relationships of the moments, derived from the initial equations, are quite simple and rapidly yield the desired results.
The study of the structure, dynamics and evolution of stellar systems forms the subject of statistical mechanics of stellar systems. Here, systems of bodies are usually considered as material points interacting in accordance with the law of mutual attraction. The most important systems are star clusters, galaxies and clusters of galaxies. The given problems lead to questions which are studied in physical kinetics. However, as distinct from studies of ordinary gases, the study of a stellar gas involves very significant characteristic features. First, a stellar gas is not at a complete statistical equilibrium. Secondly, it is important to note that the gas is situated in its own gravitation field, which should be determined together with other unknown magnitudes. Finally, the interaction between stars differs from the interaction between gas molecules in that it concerns a remote action discharge, which is analogous to the Coulomb force acting between the charged particles in a plasma. These features seriously complicate the theoretical considerations. However, in studying the motion of stars in a galaxy it is permissible to neglect the interaction at a first approximation, since the relaxation times prove to be longer than the period of time which determines the time of evolution of the Universe [1], [8].
For star clusters the relaxation time is relatively short, and it is then necessary to consider the interaction between the stars. Here the usual practice is to take advantage of the analogy between the Coulomb forces and the gravitational forces and to use Landau's kinetic equation. This equation was obtained for a plasma using the Fokker–Planck approximation (cf. Fokker–Planck equation) in representing the diffusion process in the velocity space. Landau's equation cannot give a sufficiently rigorous description of the process of evolution of a stellar system, which inevitably involves star losses. Accordingly, more general kinetic equations are employed in studying the evolution of star clusters.
One of the more important stages of astrophysical studies is to obtain the most complete and reliable information possible about the objects being studied by comparing the results obtained by observations with theoretical results. The usual practice is to study a calculated theoretical model and to check the validity of the assumptions on which its construction is based. In certain cases model representations can be dispensed with and the observed characteristics can be directly related to the theory, while reducing the number of justifiable initial assumptions to a minimum. A classical example of such an approach is the problem of finding the distribution of the spatial density of the stars from their distribution in a projection [8]. The connection between the observed and the spatial density distribution is obtained in the form of an Abel integral equation, the solution of which yields the desired result. The same equation is also obtained in a number of other problems, e.g. in the study of the distribution of atoms with respect to altitude in the chromosphere and of the electrons in the corona of the Sun. In all such cases only one assumption — on spherical symmetry — is made. A more complex integral equation is obtained in the derivation of the distribution function of the spatial velocities of the stars from the distribution of the observed radial velocities. Here, the function is reproduced in three-dimensional space from the values of its integrals in all possible planes. The examples here considered refer to so-called inverse problems. Inverse problems in astrophysics involve considerable difficulties and uncertainties both of mathematical nature and in obtaining the necessary results of observations. The mathematical aspects, in particular, have to do with possible ill-posedness of the problems. The method of regularization of the solutions of ill-posed problems proves valuable in solving many astrophysical questions.
An example of an ill-posed inverse mathematical problem in astrophysics is finding the optical properties of the atmospheres of planets by measuring their photometric characteristics. Repeated scattering of light in the atmosphere and reflections from the surface of the planet result in a loss of information on the magnitudes which determine the unknown optical properties of the atmosphere. To obtain a single-valued solution, auxiliary simplifying assumptions must be made, which strongly limit the possibilities of the investigation. Inverse mathematical problems in astrophysics often involve the solution of an integral equation
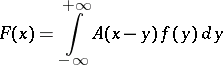 | (4) |
of the first kind, which determines the transition from the function 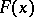 , which represents the known data about some magnitude, obtained by observations, to the unknown function
, which represents the known data about some magnitude, obtained by observations, to the unknown function 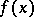 , which gives the true values of this magnitude. The results of observations may be distorted for various reasons — a fact which is quantitatively described by the function
, which gives the true values of this magnitude. The results of observations may be distorted for various reasons — a fact which is quantitatively described by the function 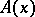 in equation (4), which is usually known for a given problem. For instance, the functions
in equation (4), which is usually known for a given problem. For instance, the functions 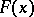 and
and 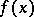 determine the experimental and the true profile of the spectral line, while the function
determine the experimental and the true profile of the spectral line, while the function 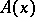 corresponds to the observed broadening profile of the ideally monochromatic spectral line, caused by the properties of the spectrograph.
corresponds to the observed broadening profile of the ideally monochromatic spectral line, caused by the properties of the spectrograph.
Many inverse problems arise in radio-astronomy both in processing the results of observations and in the interpretation of the data thus obtained. The passage from the observed distribution of temperature to the true distribution in the one-dimensional case is effected by the use of equation (4), in which 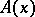 determines the property of the radio-telescope antenna and is called its diagram. An important feature of radio-astronomical studies is the use of the
determines the property of the radio-telescope antenna and is called its diagram. An important feature of radio-astronomical studies is the use of the 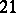 -cm radio wave-length, which is generated by the transition between the sublevels of the superfine structure of the hydrogen atom. The study of the interstellar radio-type radiation on this wave-length yields valuable information on the structure of the Galaxy and its rotation, on the distribution of the interstellar gas in it, and on the structure of the central part of the Galaxy which is inaccessible for optical methods. The line profiles observed in the various directions have a complicated shape due to various factors (thermal motion of atoms, chaotic motion of the interstellar gas, the rotation of the Galaxy, etc.). Accordingly, a number of inverse problems arise on passing from the measured to the sought characteristics. In order to eliminate the blurring effect of thermal and chaotic macroscopic movements of the gas from the observed profile, equation (4) is employed, in which
-cm radio wave-length, which is generated by the transition between the sublevels of the superfine structure of the hydrogen atom. The study of the interstellar radio-type radiation on this wave-length yields valuable information on the structure of the Galaxy and its rotation, on the distribution of the interstellar gas in it, and on the structure of the central part of the Galaxy which is inaccessible for optical methods. The line profiles observed in the various directions have a complicated shape due to various factors (thermal motion of atoms, chaotic motion of the interstellar gas, the rotation of the Galaxy, etc.). Accordingly, a number of inverse problems arise on passing from the measured to the sought characteristics. In order to eliminate the blurring effect of thermal and chaotic macroscopic movements of the gas from the observed profile, equation (4) is employed, in which 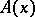 is a description of the velocity distribution. This routine systematically yields gas velocities and other magnitudes.
is a description of the velocity distribution. This routine systematically yields gas velocities and other magnitudes.
References
| [1] | V.A. Ambartsumyan, , Scientific work , 1 , Erevan (1960) (In Russian) |
| [2] | M. Schwarzschild, "Structure and evolution of stars" , Princeton Univ. Press (1958) |
| [3] | V.V. Sobolev, "A treatise on radiative transfer" , v. Nostrand (1960) (Translated from Russian) |
| [4] | V.V. Sobolev, "Course in theoretical astrophysics" , NASA , Washington, D.C. (1969) (Translated from Russian) |
| [5] | S.A. Kaplan, "Interstellar gasdynamics" , Moscow (1958) (In Russian) |
| [6] | S.B. Pikel'ner, "Fundamentals of cosmic electrodynamics" , Moscow (1966) (In Russian) |
| [7] | L. Spitzer, "Physics of fully ionized gases" , Interscience (1957) |
| [8] | S. Chandrasekhar, "Principles of stellar dynamics" , Univ. Chicago Press (1942) |
Comments
References
| [a1] | J. Ehlers (ed.) , Relativity theory and astrophysics , 1–3 , Amer. Math. Soc. (1967) |
| [a2] | R. Kurt, "Introduction to stellar statistics" , Pergamon (1967) |
| [a3] | D.A. Evano, "Mathematical cosmology" , Clarendon Press (1977) |
| [a4] | S. Chandrasekhar, "Radiative transfer" , Dover, reprint (1960) |
| [a5] | S. Chandrasekhar, "Stellar structure" , Dover, reprint (1957) |
| [a6] | S.W. Hawking, G.F.R. Ellis, "The large scale structure of space-time" , Cambridge Univ. Press (1973) |
Astrophysics, mathematical problems of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Astrophysics,_mathematical_problems_of&oldid=12968