Artinian module
From Encyclopedia of Mathematics
A module that satisfies the decreasing chain condition for submodules. The class of Artinian modules is closed with respect to passing to submodules, quotient modules, finite direct sums and extensions. Extension in this context means that if the modules 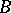 and
and 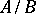 are Artinian, then so is
are Artinian, then so is 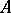 . Each Artinian module can be decomposed into a direct sum of submodules which are no longer decomposable into a direct sum. A module has a composition series if and only if it is both Artinian and Noetherian. See also Artinian ring.
. Each Artinian module can be decomposed into a direct sum of submodules which are no longer decomposable into a direct sum. A module has a composition series if and only if it is both Artinian and Noetherian. See also Artinian ring.
Comments
References
| [a1] | C. Faith, "Algebra: rings, modules, and categories" , 1 , Springer (1973) |
| [a2] | C. Faith, "Algebra" , II. Ring theory , Springer (1976) |
How to Cite This Entry:
Artinian module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Artinian_module&oldid=19017
Artinian module. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Artinian_module&oldid=19017
This article was adapted from an original article by L.A. Skornyakov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article