Arrow impossibility theorem
In 1951, K. Arrow [a1] discovered a troubling result about decisions involving three or more alternatives. After posing innocuous conditions that seemingly are satisfied by all reasonable procedures, he proved that they require a dictator. This counter-intuitive assertion is one of the better known results in the social and decision sciences; it is part of Arrow's 1972 Nobel Prize.
Arrow's first condition, unrestricted domain, allows each voter to rank the candidates in any complete, transitive manner (without ties). The Pareto condition requires that when the voters unanimously agree on the strict ranking of two candidates, then that is society's relative ranking of this pair. Independence of irrelevant alternatives, (IIA), requires society's relative ranking of a pair to depend only on how the voters rank them; it is not influenced by their views of other "irrelevant" alternatives. This condition eliminates paradoxes, where an  relative outcome can change by voters varying their
relative outcome can change by voters varying their  ranking but keeping their
ranking but keeping their  rankings fixed. Finally, the procedure has transitive outcomes.
rankings fixed. Finally, the procedure has transitive outcomes.
Arrow proved that with more than two alternatives, a dictator is the only procedure satisfying these conditions, i.e., society's ranking is determined by the dictator. If  is the set of all
is the set of all  transitive rankings of the
transitive rankings of the  candidates, then decision procedures are mappings
candidates, then decision procedures are mappings  , where a dictator is an
, where a dictator is an  that is the identity mapping on one variable; e.g., there is a component
that is the identity mapping on one variable; e.g., there is a component  so that for any profile
so that for any profile 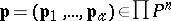 , one has
, one has 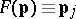 .
.
Explanation.
With the many extensions (see [a3]) and mathematical proofs of Arrow's theorem, ranging from ultrafilters to geometry [a4] to algebraic topology [a2], it is surprising that it admits an elementary explanation with a benign re-interpretation [a4], [a5]. To explain this, notice that the theorem is meaningless unless voters have transitive preferences. (For instance, if all voters had the same cyclic preferences, then Pareto forces a non-transitive outcome.) However, IIA vitiates this critical transitivity assumption. To see why, for each pair 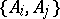 , let
, let 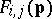 be the
be the 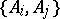 -relative ranking of
-relative ranking of  ; e.g., if
; e.g., if  , then
, then 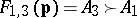 . IIA requires
. IIA requires 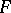 to be decomposed into the
to be decomposed into the 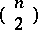 mappings
mappings 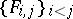 , where the
, where the 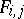 domain depends only on the voters' rankings of
domain depends only on the voters' rankings of 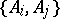 . Letting
. Letting 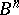 denote the set of all
denote the set of all
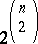 |
ways to list the strict rankings of the  pairs, IIA requires
pairs, IIA requires 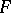 to be expressible as
to be expressible as  . This domain allows IIA-admissible procedures to be used by unsophisticated voters without transitive rankings. Similarly, the implicit independence condition conferred on the
. This domain allows IIA-admissible procedures to be used by unsophisticated voters without transitive rankings. Similarly, the implicit independence condition conferred on the 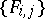 functions by IIA renders them incapable of sequencing the
functions by IIA renders them incapable of sequencing the 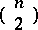 pairwise outcomes into transitivity.
pairwise outcomes into transitivity.
Thus, the transitivity assumption is a domain restriction; the goal is to identify those IIA-procedures where the 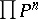 restriction is sufficiently severe to force the outcomes to be in
restriction is sufficiently severe to force the outcomes to be in 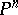 . Trivially, this includes a dictator. However, when the rankings of two or more voters are involved, some
. Trivially, this includes a dictator. However, when the rankings of two or more voters are involved, some 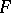 level sets contain transitive and non-transitive profiles, where the non-transitive profile determines a non-transitive
level sets contain transitive and non-transitive profiles, where the non-transitive profile determines a non-transitive 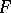 outcome. Arrow's assertion, then, holds, because IIA prohibits procedures from recognizing transitivity. This permits the alternative interpretation that rational (transitive) outcomes cannot be expected from procedures intended for highly irrational voters.
outcome. Arrow's assertion, then, holds, because IIA prohibits procedures from recognizing transitivity. This permits the alternative interpretation that rational (transitive) outcomes cannot be expected from procedures intended for highly irrational voters.
Resolution.
To resolve the problem, one replaces IIA with a condition that recognizes rational preferences. One is intensity of irrelevant alternatives (IIIA), where society's relative ranking of two candidates is determined by each voter's relative ranking and the number of alternatives separating them. Replacing Arrow's negative conclusion is that [a4], [a5] the Borda count is a procedure with transitive outcomes satisfying unrestricted domain, IIIA and Pareto. (The Borda count assigns 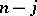 points to a voter's
points to a voter's 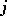 th ranked candidate,
th ranked candidate, 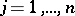 ; the candidates are ranked according to the sum of assigned points.) Thus, if rational outcomes are desired, use procedures designed for rational voters.
; the candidates are ranked according to the sum of assigned points.) Thus, if rational outcomes are desired, use procedures designed for rational voters.
References
| [a1] | K. Arrow, "Social choice and individual values" , Wiley (1963) (Edition: Second) |
| [a2] | G. Chichilnisky, "The topological equivalence of the Pareto condition and the existence of a dictator" J. Econ. Theory , 9 (1982) pp. 223–234 |
| [a3] | J. Kelly, "Social choice bibliography" Soc. Choice Welfare , 8 (1991) pp. 97–169 |
| [a4] | D.G. Saari, "Basic geometry of voting" , Springer (1995) |
| [a5] | D.G. Saari, "Arrow's and Sen's theorems revisited and resolved" Social Choice Welfare , to appear (1997) |
Arrow impossibility theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Arrow_impossibility_theorem&oldid=12728