Difference between revisions of "Arrangement"
(Importing text file) |
m (link) |
||
| Line 5: | Line 5: | ||
An arrangement can be regarded as a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342011.png" /> given on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342012.png" /> and taking values in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342013.png" />: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342014.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342015.png" />. The elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342016.png" /> are usually called cells (or urns), while those of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342017.png" /> are called particles (or balls); <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342018.png" /> defines the filling of the various cells by the various particles. If one speaks of indistinguishable particles or cells, it is understood that classes of arrangements are being considered. Thus, if all the particles are indistinguishable, then two arrangements defined by functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342019.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342020.png" />, respectively, belong to the same class if and only if there is a permutation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342021.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342022.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342023.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342024.png" />. In this case, the number of such classes, or, as it is called, the number of arrangements filling <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342025.png" /> different cells by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342026.png" /> indistinguishable particles, is the number of combinations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342027.png" /> out of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342028.png" /> elements, with repetition allowed (cf. [[Combination|Combination]]). | An arrangement can be regarded as a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342011.png" /> given on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342012.png" /> and taking values in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342013.png" />: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342014.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342015.png" />. The elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342016.png" /> are usually called cells (or urns), while those of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342017.png" /> are called particles (or balls); <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342018.png" /> defines the filling of the various cells by the various particles. If one speaks of indistinguishable particles or cells, it is understood that classes of arrangements are being considered. Thus, if all the particles are indistinguishable, then two arrangements defined by functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342019.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342020.png" />, respectively, belong to the same class if and only if there is a permutation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342021.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342022.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342023.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342024.png" />. In this case, the number of such classes, or, as it is called, the number of arrangements filling <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342025.png" /> different cells by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342026.png" /> indistinguishable particles, is the number of combinations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342027.png" /> out of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342028.png" /> elements, with repetition allowed (cf. [[Combination|Combination]]). | ||
| − | If one says that all the cells are indistinguishable, then one means that the arrangements are put into the classes in such a way that two arrangements, defined by functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342029.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342030.png" /> respectively, belong to the same class if there exists a permutation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342031.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342032.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342033.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342034.png" />. In this case the number of arrangements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342035.png" /> different particles in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342036.png" /> indistinguishable cells, that is, the number of classes, is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342037.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342038.png" /> | + | If one says that all the cells are indistinguishable, then one means that the arrangements are put into the classes in such a way that two arrangements, defined by functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342029.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342030.png" /> respectively, belong to the same class if there exists a permutation <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342031.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342032.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342033.png" /> for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342034.png" />. In this case the number of arrangements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342035.png" /> different particles in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342036.png" /> indistinguishable cells, that is, the number of classes, is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342037.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342038.png" /> are the [[Stirling numbers]] of the second kind: |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342039.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a013/a013420/a01342039.png" /></td> </tr></table> | ||
Revision as of 19:19, 21 November 2014
with repetitions of  out of
out of  elements
elements
A finite sequence  of elements from some set
of elements from some set  . If all the term of
. If all the term of  are distinct, then
are distinct, then  is called an arrangement without repetitions. The number of arrangements of
is called an arrangement without repetitions. The number of arrangements of  out of
out of  elements with repetitions is
elements with repetitions is  , and that without repetitions in
, and that without repetitions in  .
.
An arrangement can be regarded as a function 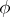 given on
given on  and taking values in
and taking values in  :
:  ,
, 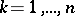 . The elements of
. The elements of  are usually called cells (or urns), while those of
are usually called cells (or urns), while those of  are called particles (or balls);
are called particles (or balls);  defines the filling of the various cells by the various particles. If one speaks of indistinguishable particles or cells, it is understood that classes of arrangements are being considered. Thus, if all the particles are indistinguishable, then two arrangements defined by functions
defines the filling of the various cells by the various particles. If one speaks of indistinguishable particles or cells, it is understood that classes of arrangements are being considered. Thus, if all the particles are indistinguishable, then two arrangements defined by functions 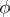 and
and 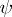 , respectively, belong to the same class if and only if there is a permutation
, respectively, belong to the same class if and only if there is a permutation 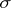 of
of 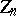 such that
such that  for all
for all  . In this case, the number of such classes, or, as it is called, the number of arrangements filling
. In this case, the number of such classes, or, as it is called, the number of arrangements filling  different cells by
different cells by  indistinguishable particles, is the number of combinations of
indistinguishable particles, is the number of combinations of  out of
out of 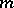 elements, with repetition allowed (cf. Combination).
elements, with repetition allowed (cf. Combination).
If one says that all the cells are indistinguishable, then one means that the arrangements are put into the classes in such a way that two arrangements, defined by functions 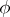 and
and 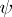 respectively, belong to the same class if there exists a permutation
respectively, belong to the same class if there exists a permutation  of
of 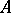 for which
for which  for all
for all  . In this case the number of arrangements of
. In this case the number of arrangements of  different particles in
different particles in  indistinguishable cells, that is, the number of classes, is
indistinguishable cells, that is, the number of classes, is  , where
, where  are the Stirling numbers of the second kind:
are the Stirling numbers of the second kind:
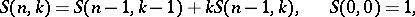 |
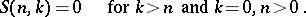 |
If one does not distinguish either particles or cells, then an arrangement of  identical particles in
identical particles in  identical cells is obtained; the number of such arrangements is
identical cells is obtained; the number of such arrangements is  , where
, where 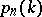 is the number of additive partitions of
is the number of additive partitions of  into
into  natural numbers. One can also consider other partitions of arrangements into classes, for example when the above-mentioned permutations
natural numbers. One can also consider other partitions of arrangements into classes, for example when the above-mentioned permutations  and
and  are taken from subgroups of the symmetric groups of degrees
are taken from subgroups of the symmetric groups of degrees  and
and  , respectively (this and other generalizations can be found in [1], [2]). Synonyms of "arrangement" are the terms "n-permutationn-permutation" , and "ordered n-sampleordered n-sample of a population" .
, respectively (this and other generalizations can be found in [1], [2]). Synonyms of "arrangement" are the terms "n-permutationn-permutation" , and "ordered n-sampleordered n-sample of a population" .
References
| [1] | A.V. Sachkov, "Combinatorial methods in discrete mathematics" , Moscow (1977) (In Russian) |
| [2] | J. Riordan, "An introduction to combinational analysis" , Wiley (1958) |
Comments
References
| [a1] | L. Comtet, "Advanced combinatorics" , Reidel (1977) (Translated from French) |
Arrangement. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Arrangement&oldid=34716