Arf-invariant
invariant of Arf
An invariant of a quadratic form modulo 2, given on an integral lattice endowed with a bilinear skew-symmetric form. Let 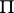 be an integral lattice of dimension
be an integral lattice of dimension 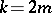 and let
and let 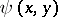 be a form for which
be a form for which 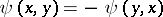 . There exists bases
. There exists bases 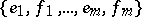 , called symplectic bases, in which the matrix of
, called symplectic bases, in which the matrix of 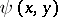 reduces to block-diagonal form: The diagonal contains the blocks
reduces to block-diagonal form: The diagonal contains the blocks
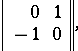 |
i.e.
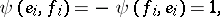 |
while the other entries are zero.
Suppose that a mapping
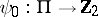 |
is given on 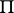 such that
such that
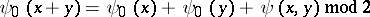 |
(a "quadratic form modulo 2" ). The expression
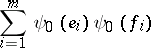 |
is then called an Arf-invariant [1]. If this expression equals zero, then there is a symplectic basis on all elements of which 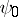 vanishes; if this expression equals one, then there is a symplectic basis on all elements of which, except
vanishes; if this expression equals one, then there is a symplectic basis on all elements of which, except 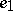 and
and 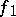 , the form
, the form  vanishes, while
vanishes, while
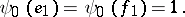 |
References
| [1] | C. Arf, "Untersuchungen über quadratischen Formen in Körpern der Charakteristik 2, I" J. Reine Angew. Math. , 183 (1941) pp. 148–167 |
Comments
See [a1], Appendix 1, for material concerning the Arf-invariant for inner product spaces over a field 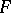 of characteristic 2 in relation to the Witt algebra of quadratic inner product spaces over
of characteristic 2 in relation to the Witt algebra of quadratic inner product spaces over 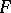 .
.
References
| [a1] | J. Milnor, D. Husemoller, "Symmetric bilinear forms" , Springer (1973) |
Arf-invariant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Arf-invariant&oldid=12338