Arens regularity
A normed algebra 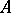 is said to be Arens regular if the pair of intrinsically defined Arens products (introduced by R. Arens in [a1] and [a2]; cf. Arens multiplication) on the double dual space
is said to be Arens regular if the pair of intrinsically defined Arens products (introduced by R. Arens in [a1] and [a2]; cf. Arens multiplication) on the double dual space 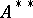 are identical. Since both Arens products extend the product on
are identical. Since both Arens products extend the product on 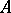 (relative to the natural embedding mapping
(relative to the natural embedding mapping 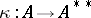 ), a Banach algebra on a reflexive Banach space (cf. also Reflexive space) is Arens regular. S. Sherman has shown [a10] that the double dual of a
), a Banach algebra on a reflexive Banach space (cf. also Reflexive space) is Arens regular. S. Sherman has shown [a10] that the double dual of a 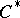 -algebra
-algebra 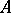 has a natural interpretation as the von Neumann algebra generated by the universal
has a natural interpretation as the von Neumann algebra generated by the universal  -representation of
-representation of 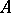 . Hence
. Hence 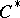 -algebras are always Arens regular.
-algebras are always Arens regular.
It is easy to show that if 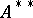 is commutative under either Arens product, then
is commutative under either Arens product, then 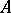 is Arens regular. The following fundamental result is due to J. Hennefeld [a5], based on work of J.S. Pym [a8] making use of Grothendieck's criterion for weak compactness.
is Arens regular. The following fundamental result is due to J. Hennefeld [a5], based on work of J.S. Pym [a8] making use of Grothendieck's criterion for weak compactness.
The following conditions are equivalent for a Banach algebra 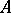 :
:
a) 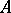 is Arens regular;
is Arens regular;
b) for each 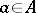 the adjoint
the adjoint 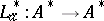 of the left regular representation is weakly compact;
of the left regular representation is weakly compact;
c) for each 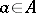 the adjoint
the adjoint 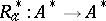 of the right regular representation is weakly compact;
of the right regular representation is weakly compact;
d) for any bounded sequences  and
and 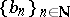 in
in 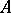 and any
and any 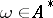 , the iterated limits
, the iterated limits
 |
are equal when they both exist.
This theorem easily implies that subalgebras and quotient algebras (with respect to closed ideals) of Arens-regular algebras are Arens regular, as first noted in [a3].
Arens regularity is rare among general Banach algebras. N.J. Young [a11] has shown that for a locally compact group (cf. also Compact group; Locally compact skew-field)  ,
, 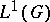 (or
(or 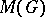 ) is Arens regular if and only if
) is Arens regular if and only if 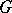 is finite. P. Civin and B. Yood had proved this for Abelian groups in [a3]. In [a12] it is shown that the measure algebra (cf. Algebra of measures)
is finite. P. Civin and B. Yood had proved this for Abelian groups in [a3]. In [a12] it is shown that the measure algebra (cf. Algebra of measures) 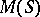 of a locally compact semi-group
of a locally compact semi-group 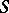 in which multiplication is at least singly continuous is Arens regular if and only if
in which multiplication is at least singly continuous is Arens regular if and only if 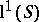 is. These are, in turn, equivalent to either:
is. These are, in turn, equivalent to either:
there do not exist sequences 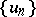 and
and 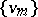 in
in 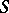 such that the sets
such that the sets 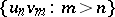 and
and 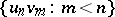 are disjoint;
are disjoint;
the semi-group operation can be extended to the Stone–Čech compactification 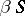 of
of 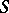 as a discrete space.
as a discrete space.
In [a13], Young has proved that the algebra 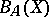 of approximable operators (i.e., those uniformly approximable by finite-rank operators) on a Banach space
of approximable operators (i.e., those uniformly approximable by finite-rank operators) on a Banach space 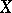 is regular if and only if
is regular if and only if 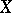 is reflexive (cf. Reflexive space). Hence, if the Banach algebra
is reflexive (cf. Reflexive space). Hence, if the Banach algebra 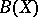 of all bounded linear operators on a Banach space
of all bounded linear operators on a Banach space 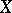 is Arens regular, then
is Arens regular, then 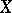 must be reflexive. He also shows that there are reflexive Banach spaces
must be reflexive. He also shows that there are reflexive Banach spaces 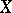 with
with 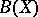 not Arens regular.
not Arens regular.
Á. Rodriguez-Palacios [a9] has shown that any (even non-associative) continuous multiplication on a Banach space 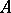 is Arens regular if and only if every bounded linear mapping from
is Arens regular if and only if every bounded linear mapping from  into
into 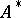 is weakly compact (cf. Weak topology).
is weakly compact (cf. Weak topology). 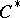 -algebras satisfy this criterion.
-algebras satisfy this criterion.
A weaker version of Arens regularity was introduced by M. Grosser [a4]. An approximately unital Banach algebra 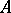 is said to be semi-regular if it satisfies
is said to be semi-regular if it satisfies 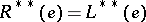 for all mixed identities
for all mixed identities  . (An element
. (An element 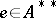 is called a mixed identity if it is simultaneously a right identity for the first Arens product and a left identity for the second Arens product, see Arens multiplication.) He shows that an Arens-regular algebra is semi-regular and that any commutative approximately unital Banach algebra is semi-regular.
is called a mixed identity if it is simultaneously a right identity for the first Arens product and a left identity for the second Arens product, see Arens multiplication.) He shows that an Arens-regular algebra is semi-regular and that any commutative approximately unital Banach algebra is semi-regular.
The most comprehensive recent (1996) exposition is [a7], which contains numerous further references.
References
| [a1] | R. Arens, "Operations induced in function classes" Monatsh. Math. , 55 (1951) pp. 1–19 |
| [a2] | R. Arens, "The adjoint of a bilinear operation" Proc. Amer. Math. Soc. , 2 (1951) pp. 839–848 |
| [a3] | P. Civin, B. Yood, "The second conjugate space of a Banach algebra as an algebra" Pacific J. Math. , 11 (1961) pp. 847–870 |
| [a4] | M. Grosser, "Arens semiregular Banach algebras" Monatsh. Math. , 98 : 1 (1984) pp. 41–52 |
| [a5] | J.O. Hennefeld, "A note on the Arens products" Pacific J. Math. , 26 (1968) pp. 115–119 |
| [a6] | S. Kaijser, "On Banach modules I" Math. Proc. Cambridge Philos. Soc. , 90 : 3 (1981) pp. 423–444 |
| [a7] | T.W. Palmer, "Banach algebras and the general theory of  -algebras I" , Encycl. Math. Appl. , 49 , Cambridge Univ. Press (1994) -algebras I" , Encycl. Math. Appl. , 49 , Cambridge Univ. Press (1994) |
| [a8] | J.S. Pym, "The convolution of functionals on spaces of bounded functions" Proc. London Math. Soc. (3) , 15 (1965) pp. 84–104 |
| [a9] | Á. Rodriguez-Palacios, "A note on Arens regularity" Quart. J. Math. Oxford Ser. (2) , 38 : 149 (1987) pp. 1991–1993 |
| [a10] | S. Sherman, "The second adjoint of a 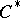 -algebra" , Proc. Internat. Congress Math. Cambridge, I (1950) pp. 470 -algebra" , Proc. Internat. Congress Math. Cambridge, I (1950) pp. 470 |
| [a11] | N.J. Young, "The irregularity of multiplication in group algebras" Quart. J. Math. Oxford Ser. (2) , 24 (1973) pp. 59–62 |
| [a12] | N.J. Young, "Semigroup algebras having regular multiplication" Studia Math. , 47 (1973) pp. 191–196 |
| [a13] | N.J. Young, "Periodicity of functionals and representations of normed algebras on reflexive spaces" Proc. Edinburgh Math. Soc. (2) , 20 : 2 (1976–77) pp. 99–120 |
Arens regularity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Arens_regularity&oldid=13185