Area function
From Encyclopedia of Mathematics
The set function on a sphere  equal to the area
equal to the area  of that part of the convex surface
of that part of the convex surface  that has spherical image
that has spherical image  . This definition remains meaningful for general convex surfaces and it gives a totally-additive set function on the ring of Borel sets.
. This definition remains meaningful for general convex surfaces and it gives a totally-additive set function on the ring of Borel sets.
References
| [1] | A.D. Aleksandrov, Mat. Sb. , 3 : 1 (1938) pp. 27–44 |
| [2] | H. Busemann, "Convex surfaces" , Interscience (1958) |
Comments
In the article,  is the unit sphere in
is the unit sphere in  with centre at the origin. If one associates to each point
with centre at the origin. If one associates to each point  the unit normal vector
the unit normal vector  and shifts this vector
and shifts this vector  so that its base coincides with the origin, then the end point of
so that its base coincides with the origin, then the end point of  is a point
is a point 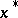 on
on  . The point
. The point 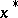 is called the spherical image of
is called the spherical image of  . The procedure for obtaining the spherical image of a point goes under the name of spherical mapping, cf. Spherical map.
. The procedure for obtaining the spherical image of a point goes under the name of spherical mapping, cf. Spherical map.
How to Cite This Entry:
Area function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Area_function&oldid=11860
Area function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Area_function&oldid=11860
This article was adapted from an original article by M.I. Voitsekhovskii (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article