Area
A numerical characteristic assigned to planar figures of a certain class (for example, polygons) and having the following properties: 1) the area is non-negative; 2) the area is additive (in the case of polygons this means that if a figure 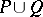 is composed of two figures
is composed of two figures 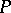 and
and 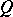 not having common interior points, then
not having common interior points, then 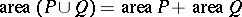 ); 3) the area is preserved under displacements; and 4) the area of the unit square is 1. The term "area" is used also in a more general sense as a numerical characteristic of two-dimensional surfaces in three-dimensional space, for
); 3) the area is preserved under displacements; and 4) the area of the unit square is 1. The term "area" is used also in a more general sense as a numerical characteristic of two-dimensional surfaces in three-dimensional space, for  -dimensional surfaces in an
-dimensional surfaces in an  -dimensional Euclidean or Riemannian space
-dimensional Euclidean or Riemannian space  , and for the boundaries of sets and other objects, see below.
, and for the boundaries of sets and other objects, see below.
The area of a planar figure.
Historically, the area was determined initially on the class of polygons (figures having a decomposition into a finite number of triangles without common interior points). It is important that an area with the properties 1)–4) exists and is unique in the class of polygons [1], [2]. One of the consequences of 1)–4) is that the area of an entire figure is not less than the area of its parts.
In Antiquity, the existence and uniqueness of the area with properties 1)–4) was assumed without an explicit description of the class of figures; attention was concentrated on ways of calculating the area. The formula for the area of a rectangle, including one with irrational sides, was based on the method of exhaustion (cf. Exhaustion, method of). The area of a triangle or of any polygon was calculated as the area of the rectangle such that the given triangle or polygon and the rectangle are both built up from the same congruent parts. It has been shown [2] that any polygons of equal area are decomposable into the same congruent parts.
Later, the class of squarable (Jordan-measurable) figures was distinguished. A figure  in the plane is said to be squarable if for any
in the plane is said to be squarable if for any 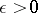 there exist polygonal figures
there exist polygonal figures 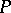 and
and 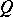 such that
such that 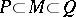 and
and 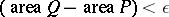 . The class of squarable figures is extremely rich. It includes, in particular, all bounded domains in the plane with piecewise-smooth boundaries. However, there are also non-squarable planar figures. In the class of squarable figures, an area with the properties 1)–4) exists and is unique [2].
. The class of squarable figures is extremely rich. It includes, in particular, all bounded domains in the plane with piecewise-smooth boundaries. However, there are also non-squarable planar figures. In the class of squarable figures, an area with the properties 1)–4) exists and is unique [2].
Historically, before the class of squarable figures was considered, people knew how to calculate the areas of some of them: the disc, a circular sector and segments, various kinds of choral figures, and curvilinear trapezia. These calculations were based on the method of exhaustion by polygons. In some cases, Cavalieri's principle (cf. Cavalieri principle) was used as the basis for such calculations. It states that if two planar figures of this type intersect every line parallel to a given one in segments of identical length, then these figures are equal in area. Techniques in integral calculus (see, for example, [3]) give convenient methods of calculating the area of any planar domain with a piecewise-smooth boundary. The integral calculus justifies Cavalieri's principle.
Attempts to extend the concept of area to more general planar sets while retaining the properties 1)–4) led to measure theory and to the distinction of the class of planar Lebesgue-measurable sets. The transition to even more general classes of sets in the plane leads to non-unique measures with the properties 1)–4).
Oriented area.
If there is a directed closed curve 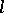 in the oriented plane, possibly with self-intersections and overlaps, then for each point in the plane not lying on
in the oriented plane, possibly with self-intersections and overlaps, then for each point in the plane not lying on 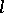 there is an integer function (positive, negative or zero), called the degree of the point with respect on
there is an integer function (positive, negative or zero), called the degree of the point with respect on  . It indicates how many times and in what direction the contour
. It indicates how many times and in what direction the contour 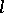 encircles that point. The integral over the entire plane of this function, if it exists, is called the oriented area enclosed by
encircles that point. The integral over the entire plane of this function, if it exists, is called the oriented area enclosed by 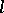 . The latter differs from the ordinary area in having a sign. See [4] for simple properties of an oriented area.
. The latter differs from the ordinary area in having a sign. See [4] for simple properties of an oriented area.
The area of surfaces.
The areas of polyhedral surfaces are first and most simply defined as the sums of the areas of the planar faces. There are difficulties in attempts to introduce the concept of area for curved surfaces as the limit of the areas of inscribed polyhedral surfaces (in a similar was as the length of a curve is defined as the limit of inscribed polygonal lines). Even for a very simple curved surface, the areas of inscribed polyhedra with successively smaller faces may have different limits, depending on the choice of the sequence of polyhedra. This is clearly demonstrated by Schwartz' example, in which sequences of inscribed polyhedra with different limits of the area are constructed for the lateral surface of a right circular cylinder [2].
Most frequently, the area of surfaces is defined for the class of piecewise-smooth surfaces with piecewise-smooth boundaries (or without boundary). Usually, this is based on the following construction. The surface is split up into small parts with piecewise-smooth boundaries. In each part one selects a point at which the tangent plane exists and projects the part orthogonally on the tangent plane to the surface at that point; the areas of the resulting planar projections are summed, and finally one passes to the limit for increasingly fine subdivisions (such that the largest of the diameters in the parts of the subdivision tends to zero). This limit always exists in the class of surfaces, and if the surface is given parametrically by a piecewise 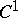 -smooth function
-smooth function 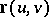 , where the parameters
, where the parameters  and
and  vary in a domain
vary in a domain 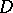 in the
in the 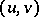 -plane, then the area
-plane, then the area 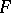 is expressed by the double integral
is expressed by the double integral
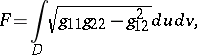 | (1) |
where 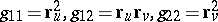 , while
, while  and
and 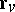 are the partial derivatives with respect to
are the partial derivatives with respect to  and
and  . The proof is given, for example, in [3], [5]. In particular, if the surface is the graph of a
. The proof is given, for example, in [3], [5]. In particular, if the surface is the graph of a 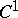 -smooth function
-smooth function 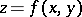 over a domain
over a domain 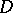 in the
in the 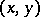 -plane, then
-plane, then
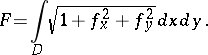 | (2) |
Here 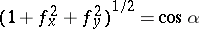 , where
, where  is the (acute) angle between the normal to the surface and the
is the (acute) angle between the normal to the surface and the  -axis. From (1) and (2) one gets the standard formulas for the area of a sphere or parts of it, as well as methods for calculating the areas of surfaces of rotation, etc.
-axis. From (1) and (2) one gets the standard formulas for the area of a sphere or parts of it, as well as methods for calculating the areas of surfaces of rotation, etc.
For two-dimensional piecewise-smooth surfaces in Riemannian manifolds [6], formula (1) serves as a definition of the area, where the roles of 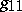 ,
, 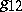 and
and  are played by the components of the metric tensor restricted to the surface itself.
are played by the components of the metric tensor restricted to the surface itself.
It is important that even in the case of a two-dimensional surface, the area is assigned not to the set of points but to the equivalence class of mappings representing the two-dimensional manifold into a space, and thus differs from a measure.
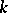 -dimensional area.
-dimensional area.
For a piecewise-smooth immersion 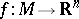 of a
of a 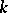 -dimensional manifold (with or without boundary) into
-dimensional manifold (with or without boundary) into  -dimensional Euclidean space,
-dimensional Euclidean space,  , the area is defined by means of a construction that is completely analogous to that described above for piecewise-smooth surfaces. The only difference is that the projection now involves
, the area is defined by means of a construction that is completely analogous to that described above for piecewise-smooth surfaces. The only difference is that the projection now involves 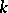 -dimensional tangent planes and that the summation is over the
-dimensional tangent planes and that the summation is over the 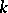 -dimensional projection volumes. If one has introduced coordinates
-dimensional projection volumes. If one has introduced coordinates 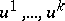 in a domain
in a domain 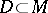 , then the area
, then the area 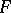 of the immersion
of the immersion 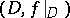 is expressed by the integral
is expressed by the integral
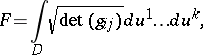 | (3) |
where 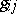 are the scalar products
are the scalar products 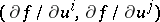 . If
. If 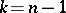 and
and 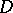 is a domain in the coordinate hyperplane
is a domain in the coordinate hyperplane 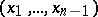 , while
, while 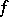 has the explicit form
has the explicit form 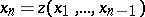 , (3) becomes
, (3) becomes
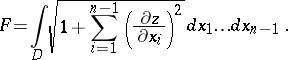 | (4) |
If 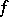 is a smooth mapping, then the
is a smooth mapping, then the 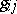 are the coefficients of the metric tensor induced by the immersion, and it follows from (3) that the area defined by the external construction belongs to the intrinsic geometry of the immersed manifold. In general, (3) is taken as the definition of area in the case of an immersion not only into
are the coefficients of the metric tensor induced by the immersion, and it follows from (3) that the area defined by the external construction belongs to the intrinsic geometry of the immersed manifold. In general, (3) is taken as the definition of area in the case of an immersion not only into  but also into a Riemannian manifold.
but also into a Riemannian manifold.
On the class of piecewise-smooth immersed manifolds, the area is: a) non-negative; b) equal to 1 on the 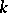 -dimensional unit cube in
-dimensional unit cube in 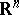 ; c) preserved under orthogonal transformations; d) additive; e) semi-continuous, i.e.
; c) preserved under orthogonal transformations; d) additive; e) semi-continuous, i.e. 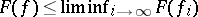 if
if 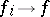 uniformly. Further: f) if
uniformly. Further: f) if 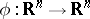 is a non-stretching mapping, then
is a non-stretching mapping, then 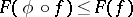 ; and g) if
; and g) if 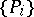 is a set of
is a set of  pairwise-orthogonal
pairwise-orthogonal 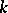 -dimensional planes and if
-dimensional planes and if  is the projection onto
is the projection onto 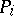 , then
, then
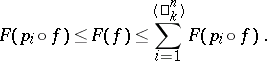 | (5) |
Further extensions. The theory of area.
The extension of 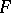 to more general objects while retaining some of properties a)–g) is possible in various ways and leads to various results. The theory of area deals with these extensions. See [10] for a review of the relations between various concepts of area.
to more general objects while retaining some of properties a)–g) is possible in various ways and leads to various results. The theory of area deals with these extensions. See [10] for a review of the relations between various concepts of area.
The boundary between the theory of area and measure theory is not clear-cut. Traditionally, the theory of area relates primarily to the study of the areas of continuous mappings, where multiplicity is taken into account and the preservation of additivity is less important. See, for example, Hausdorff measure; Favard measure or  -dimensional measures in
-dimensional measures in  -dimensional space.
-dimensional space.
An area can be introduced on the basis of an approximating, integral-geometric, or functional approach or else axiomatically. The most common concepts are given below.
The Lebesgue area.
It (cf. [7], [9]) is defined by
 | (6) |
where 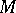 is a finitely-triangulable
is a finitely-triangulable  -dimensional manifold,
-dimensional manifold, 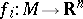 are all possible sequences of piecewise-linear mappings with
are all possible sequences of piecewise-linear mappings with 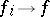 , and
, and 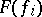 is the
is the 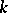 -dimensional area of the corresponding polyhedral surface. The Lebesgue area is the same for Fréchet-equivalent mappings and therefore is a characteristic of a Fréchet surface.
-dimensional area of the corresponding polyhedral surface. The Lebesgue area is the same for Fréchet-equivalent mappings and therefore is a characteristic of a Fréchet surface.
If 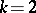 , the condition
, the condition 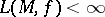 implies various useful properties of the surface (for example, the possibility of introducing isothermal parameters); in that case, the Lebesgue area is a convenient tool sufficient to solve the Plateau problem and more general two-dimensional problems in variational calculus. There arise difficulties in the investigation of variational problems for the class of continuous mappings for
implies various useful properties of the surface (for example, the possibility of introducing isothermal parameters); in that case, the Lebesgue area is a convenient tool sufficient to solve the Plateau problem and more general two-dimensional problems in variational calculus. There arise difficulties in the investigation of variational problems for the class of continuous mappings for 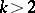 (the compactness problem), which has led to the search for other objects (currents and varifolds) and related characteristics of area type. The use of the Lebesgue area is restricted also by the complexity in establishing its relationships to other concepts of area and certain of its properties (for example, the right-hand inequality in (5)). There are two notable features of
(the compactness problem), which has led to the search for other objects (currents and varifolds) and related characteristics of area type. The use of the Lebesgue area is restricted also by the complexity in establishing its relationships to other concepts of area and certain of its properties (for example, the right-hand inequality in (5)). There are two notable features of  : for
: for 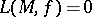 it may happen that the volume
it may happen that the volume 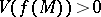 , and, secondly, even for
, and, secondly, even for 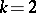 , decomposing
, decomposing 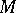 into
into 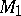 and
and 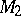 with a common boundary in the form of a curve, it may happen that
with a common boundary in the form of a curve, it may happen that
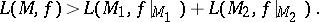 | (7) |
Studies have also been made concerning which of the properties a)–g) can be retained when additivity is replaced by semi-additivity, e.g. assuming an inequality of the type of (7) one still gets the Lebesgue area. Topics of this type have not yet (1983) been examined completely [7].
Integral-geometric areas.
(Cf. [9].) Let 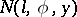 be some multiplicity function for mappings
be some multiplicity function for mappings 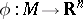 at a point
at a point 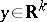 , for example
, for example 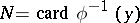 . Then for
. Then for 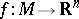 , one may define the integral-geometric area
, one may define the integral-geometric area
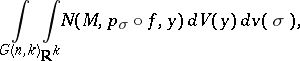 | (8) |
where 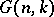 is the Grassmann manifold of
is the Grassmann manifold of 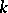 -dimensional subspaces
-dimensional subspaces 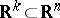 ,
,  is the normalized Haar measure on
is the normalized Haar measure on 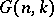 and
and 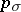 are the orthogonal projections on
are the orthogonal projections on 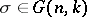 . The areas (8) may differ for various multiplicity functions. A very special choice of
. The areas (8) may differ for various multiplicity functions. A very special choice of 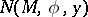 makes (8) coincide with the Lebesgue area for
makes (8) coincide with the Lebesgue area for 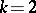 for triangulable
for triangulable 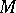 , as well as for
, as well as for 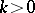 if the Hausdorff measure
if the Hausdorff measure 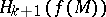 vanishes completely [9]. For the case
vanishes completely [9]. For the case 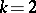 , various integral-geometric areas have been introduced also by G. Peano, Hetz and S. Banach [7].
, various integral-geometric areas have been introduced also by G. Peano, Hetz and S. Banach [7].
The area of the boundary of a set.
The Minkowski area was introduced in connection with the proof of the Brunn–Minkowski inequality and the classical isoperimetric inequality. It is assigned to a set 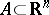 , but characterizes the area of the boundary, and is defined by
, but characterizes the area of the boundary, and is defined by
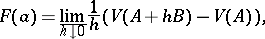 | (9) |
where 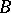 is the unit sphere in
is the unit sphere in 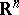 and
and 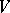 denotes the volume. For sets
denotes the volume. For sets 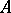 with a piecewise-smooth boundary and for convex sets
with a piecewise-smooth boundary and for convex sets 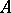 , the ordinary limit in (9) exists; it coincides with the
, the ordinary limit in (9) exists; it coincides with the 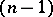 -dimensional area of the boundary. Definition (9) still applies to sets in finite-dimensional normed spaces, where the area (9) may differ from the Hausdorff measure
-dimensional area of the boundary. Definition (9) still applies to sets in finite-dimensional normed spaces, where the area (9) may differ from the Hausdorff measure 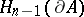 even for convex sets
even for convex sets 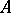 .
.
There is another useful characteristic analogous to area, which is put into correspondence with a set, but which characterizes mainly the boundary, namely the perimeter of a measurable set. This is a particular case of the concept of a current mass.
Intrinsic area.
If  is metrized and
is metrized and 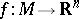 is a locally isometric mapping, one has to consider the relation between
is a locally isometric mapping, one has to consider the relation between 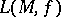 and the Hausdorff measure
and the Hausdorff measure 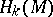 . When
. When 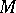 is a two-dimensional manifold of bounded curvature, one has
is a two-dimensional manifold of bounded curvature, one has 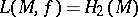 . In general, on the other hand, a continuous
. In general, on the other hand, a continuous 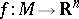 induces a generalized metric
induces a generalized metric 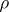 distinguished by the possibility
distinguished by the possibility  on the connected components
on the connected components 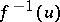 ,
,  . The construction of the
. The construction of the 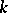 -dimensional Hausdorff measure applied to
-dimensional Hausdorff measure applied to 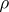 gives a characteristic that can be taken as the intrinsic area of an immersion. For
gives a characteristic that can be taken as the intrinsic area of an immersion. For 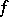 in a Lipschitz class, this coincides with
in a Lipschitz class, this coincides with 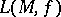 [11].
[11].
Current masses and varifolds.
The integration of 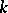 -forms with respect to a
-forms with respect to a  -dimensional piecewise-smooth oriented manifold
-dimensional piecewise-smooth oriented manifold 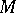 imbedded in
imbedded in 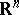 leads to the current
leads to the current 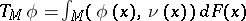 , being a linear functional of the
, being a linear functional of the 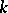 -forms
-forms  on
on 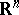 . Here
. Here  is a unit
is a unit 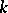 -vector tangent to
-vector tangent to  . The linear functional
. The linear functional 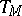 essentially characterizes
essentially characterizes 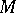 . Also, a non-linear functional can be defined (in the same way and for non-oriented
. Also, a non-linear functional can be defined (in the same way and for non-oriented 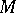 ): the varifold
): the varifold 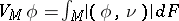 . The integral norm (masses)
. The integral norm (masses) 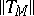 and
and  coincide with the area, i.e. with
coincide with the area, i.e. with  . The inclusion of the class of piecewise-smooth submanifolds of
. The inclusion of the class of piecewise-smooth submanifolds of 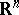 in more general current and varifold classes plays the same role in variational calculus as do generalized solutions in the theory of partial differential equations.
in more general current and varifold classes plays the same role in variational calculus as do generalized solutions in the theory of partial differential equations.
There are extensive classes of integer currents and varifolds among all of these. These retain many geometric properties of submanifolds. For example, an integer-valued current is a current having a representation  , where
, where 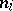 are integers and
are integers and 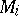 are
are  -smooth submanifolds, subject to the condition that the mass of the
-smooth submanifolds, subject to the condition that the mass of the 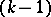 -dimensional current
-dimensional current 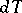 defined by
defined by 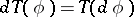 is finite. The masses of integer-valued currents and varifolds can be considered as an extension of the concept of the area of a surface. Here again, there is a relationship to the Lebesgue area. Let piecewise-smooth mappings
is finite. The masses of integer-valued currents and varifolds can be considered as an extension of the concept of the area of a surface. Here again, there is a relationship to the Lebesgue area. Let piecewise-smooth mappings 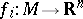 converge uniformly,
converge uniformly, 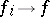 , and let
, and let 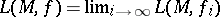 . Then the corresponding varifolds
. Then the corresponding varifolds 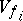 converge weakly to some integer-valued varifold
converge weakly to some integer-valued varifold 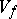 , where
, where 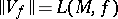 . Thus, each
. Thus, each 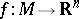 with
with 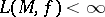 is naturally put into correspondence with a varifold
is naturally put into correspondence with a varifold 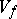 with mass
with mass 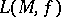 ; see [13] for this in the language of currents.
; see [13] for this in the language of currents.
References
| [1] | H. Lebesgue, "Sur la mesure des grandeurs" Monogr. de l'Enseign. Math. , 1 (1935) |
| [2] | , Encyclopaedia of elementary mathematics , 5 , Moscow (1966) (In Russian) |
| [3] | V.A. Il'in, E.G. Poznyak, "Fundamentals of mathematical analysis" , 1–2 , MIR (1982) (Translated from Russian) |
| [4] | A.M. Lopshits, "Calculating the area of oriented figures" , Moscow (1956) (In Russian) |
| [5] | A.V. Pogorelov, "Differential geometry" , Noordhoff (1959) (Translated from Russian) |
| [6] | P.K. [P.K. Rashevskii] Rashewski, "Riemannsche Geometrie und Tensoranalyse" , Deutsch. Verlag Wissenschaft. (1959) (Translated from Russian) |
| [7] | L. Cesari, "Surface area" , Princeton Univ. Press (1956) |
| [8] | H. Federer, "Geometric measure theory" , Springer (1969) |
| [9] | H. Federer, "Measure and area" Bull. Amer. Math. Soc. , 58 : 3 (1952) pp. 306–378 |
| [10] | Yu.D. Burago, V.A. Zalgaller, "Geometric inequalities" , Springer (1988) (Translated from Russian) |
| [11] | H. Busemann, "Intrinsic area" Ann. of Math. Ser. 2 , 48 (1947) pp. 234–267 |
| [12] | F.J. Almgren, "The theory of varifolds" , Princeton Univ. Press (1965) |
| [13] | H. Federer, "Currents and area" Trans. Amer. Math. Soc. , 98 : 2 (1961) pp. 204–233 |
Area. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Area&oldid=18328