Arcsine law
A limit theorem describing the fluctuations of a random walk on the real line, which results in an arcsine distribution or a generalized arcsine distribution. The following feature of a Brownian motion 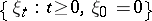 was noted in 1939 by P. Lévy. Let
was noted in 1939 by P. Lévy. Let  be the Lebesgue measure of the set
be the Lebesgue measure of the set  or, in other words, the time spent by a Brownian particle on the positive semi-axis during the interval of time
or, in other words, the time spent by a Brownian particle on the positive semi-axis during the interval of time  . The ratio
. The ratio  will then have the arcsine distribution:
will then have the arcsine distribution:
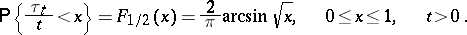 |
It was subsequently noted [2] that a random walk with discrete time obeys the following arcsine law: Let  be the successive locations in the random walk,
be the successive locations in the random walk,
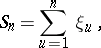 |
where  are independent and identically distributed, let
are independent and identically distributed, let  be equal to the number of indices
be equal to the number of indices 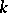 among
among 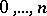 for which
for which 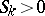 , and let
, and let
 |
then the relationships
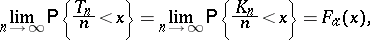 |
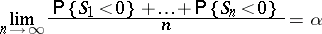 |
are all satisfied or not satisfied at the same time; here, 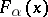 for
for  is the generalized arcsine distribution,
is the generalized arcsine distribution,
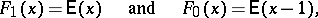 |
where 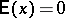 if
if 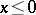 and
and 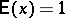 if
if 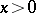 .
.
The arcsine law in renewal theory states that for 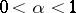 the following equalities are valid:
the following equalities are valid:
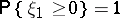 |
and for
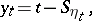 |
where 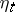 is defined by the relation
is defined by the relation 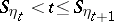 ,
,
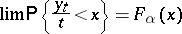 |
if and only if
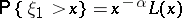 |
for  , where
, where 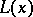 is a function which is defined for
is a function which is defined for  and which has the property
and which has the property
 |
There exists a close connection between the arcsine law in renewal theory and the arcsine law governing a random walk [3].
References
| [1] | W. Feller, "An introduction to probability theory and its applications" , 2 , Wiley (1971) |
| [2] | F. Spitzer, "Principles of random walk" , Springer (1976) |
| [3] | B.A. Rogozin, "The distribution of the first ladder moment and height and fluctuation of a random walk" Theory Probab. Appl. , 16 : 4 (1971) pp. 575–595 Teor. Veroyatnost. i Primenen. , 16 : 4 (1971) pp. 593–613 |
Comments
The function 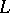 in the article above is called a slowly varying function, cf. [1], p. 269.
in the article above is called a slowly varying function, cf. [1], p. 269.
Arcsine law. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Arcsine_law&oldid=18102