Approximation of functions of several real variables
The case when the function 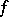 to be approximated depends on two or more variables:
to be approximated depends on two or more variables:
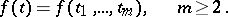 |
(See Approximation of functions.) In comparison with the one-dimensional case, the study of problems on the approximation of functions of  (
(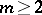 ) variables is highly complicated because of essentially new circumstances that arise related to dimension. First of all this applies to the domain on which the approximation is carried out. Simply-connected compact sets (in the one-dimensional case intervals) in
) variables is highly complicated because of essentially new circumstances that arise related to dimension. First of all this applies to the domain on which the approximation is carried out. Simply-connected compact sets (in the one-dimensional case intervals) in 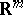 (even in the plane) can have a large variety of shapes; therefore it becomes necessary to classify the domains according to, for instance, the smoothness properties of their boundaries. Complications also arise in the description of difference-differential properties of functions of
(even in the plane) can have a large variety of shapes; therefore it becomes necessary to classify the domains according to, for instance, the smoothness properties of their boundaries. Complications also arise in the description of difference-differential properties of functions of 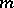 variables. Generally speaking, these properties can be different in different directions, and their characterization ought to take into account both the geometry of the domain on which the function is defined and the behaviour of the function while approaching the boundary, so that the study of boundary properties of the function is of great importance. If one attempts to simplify the solution of an approximation problem by passing to a domain with a simpler structure, the problem that arises is to extend a function
variables. Generally speaking, these properties can be different in different directions, and their characterization ought to take into account both the geometry of the domain on which the function is defined and the behaviour of the function while approaching the boundary, so that the study of boundary properties of the function is of great importance. If one attempts to simplify the solution of an approximation problem by passing to a domain with a simpler structure, the problem that arises is to extend a function 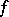 from a domain
from a domain 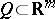 into a canonical domain
into a canonical domain 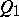 (for instance a parallelepiped or the whole space
(for instance a parallelepiped or the whole space 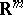 ) containing
) containing 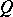 while preserving certain smoothness properties (see Extension theorems). This kind of problems is closely connected with imbedding theorems, and also with questions arising in the solution of the boundary value problems of mathematical physics.
while preserving certain smoothness properties (see Extension theorems). This kind of problems is closely connected with imbedding theorems, and also with questions arising in the solution of the boundary value problems of mathematical physics.
An increase in the number of independent variables complicates, of course, also the tools of approximation, because when the dimension is increased, with it, e.g., the degrees of the polynomials increase. An algebraic polynomial of degrees 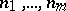 in the variables
in the variables 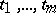 , respectively, has the form
, respectively, has the form
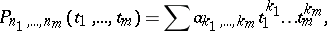 | (1) |
where  are real coefficients. The summation is carried out with respect to
are real coefficients. The summation is carried out with respect to 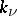 ,
, 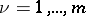 , from 0 to
, from 0 to 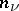 , so that, e.g., the subspace of polynomials of degree 3 in each of the
, so that, e.g., the subspace of polynomials of degree 3 in each of the 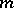 variables has dimension
variables has dimension 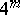 . Sometimes the overall or total degree
. Sometimes the overall or total degree  of the polynomial is fixed; then the summation in (1) is carried out over all indices satisfying the inequality
of the polynomial is fixed; then the summation in (1) is carried out over all indices satisfying the inequality 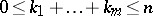 . A real trigonometric polynomial of degrees
. A real trigonometric polynomial of degrees 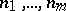 in the variables
in the variables 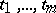 can be written in the form
can be written in the form
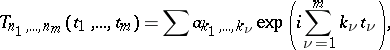 |
where complex coefficients 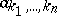 with indices of opposite sign are complex conjugate, and the summation is carried out with respect to
with indices of opposite sign are complex conjugate, and the summation is carried out with respect to 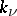 ,
, 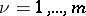 , from
, from  to
to 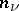 . Such a polynomial can be represented in the form of a linear combination of all possible products of the form
. Such a polynomial can be represented in the form of a linear combination of all possible products of the form 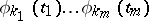 , where
, where 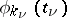 is either
is either 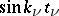 (
(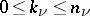 ) or
) or 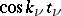 (
( ). Multi-dimensional splines have a wide field of applications; they consist of "pieces" of algebraic polynomials in
). Multi-dimensional splines have a wide field of applications; they consist of "pieces" of algebraic polynomials in 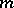 variables "tied" together in order to obtain specified smoothness properties. In the case
variables "tied" together in order to obtain specified smoothness properties. In the case 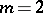 , splines of the simplest form are formed by polynomials "tied" together along straight lines parallel to the coordinate axes. As a tool of approximation functions
, splines of the simplest form are formed by polynomials "tied" together along straight lines parallel to the coordinate axes. As a tool of approximation functions 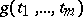 are used which are polynomials or splines only in one of the variables. For the approximation of non-periodic functions given on the whole space
are used which are polynomials or splines only in one of the variables. For the approximation of non-periodic functions given on the whole space 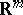 (or on an unbounded subset of
(or on an unbounded subset of 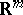 ) one may use entire functions of exponential type. These can be represented in the form of sums of absolutely convergent power series
) one may use entire functions of exponential type. These can be represented in the form of sums of absolutely convergent power series
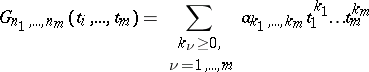 | (2) |
under the condition that for any 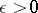 and all complex
and all complex 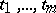 one has
one has
 |
where the constant 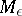 depends only on
depends only on  (see [1]). It should be noted that, unlike polynomials, the function (2) is determined by an infinite number of parameters.
(see [1]). It should be noted that, unlike polynomials, the function (2) is determined by an infinite number of parameters.
In the multi-dimensional case one has Weierstrass' theorem on the possibility of approximating a function 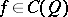 , i.e. continuous on a bounded and closed set
, i.e. continuous on a bounded and closed set 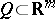 , or a function
, or a function 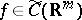 , continuous on the whole space
, continuous on the whole space 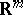 with period
with period  in each variable, with arbitrary accuracy by means of algebraic (respectively, trigonometric) polynomials. A similar result holds in the spaces
in each variable, with arbitrary accuracy by means of algebraic (respectively, trigonometric) polynomials. A similar result holds in the spaces 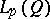 and
and 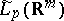 (in the periodic case) (
(in the periodic case) (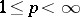 ). General results and theorems concerning properties of the best approximation, the existence and uniqueness, the characteristic properties of functions of best approximation, and general relations of duality when approximating by (means of) a convex set (of functions) and, in particular, by a subspace, can be extended to normed linear spaces of functions of
). General results and theorems concerning properties of the best approximation, the existence and uniqueness, the characteristic properties of functions of best approximation, and general relations of duality when approximating by (means of) a convex set (of functions) and, in particular, by a subspace, can be extended to normed linear spaces of functions of 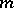 variables (see [3] and [4]). However, to obtain explicit formulations of these theorems, taking into account a specific metric and specific properties of the approximating subspace in the multi-dimensional case, involves great difficulties.
variables (see [3] and [4]). However, to obtain explicit formulations of these theorems, taking into account a specific metric and specific properties of the approximating subspace in the multi-dimensional case, involves great difficulties.
Quite thorough investigations were carried out on questions concerning the connection between the smoothness properties of a function of several variables and the rate of decrease of its best approximation by algebraic and trigonometric polynomials, as well as by entire functions.
Let 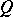 be an arbitrary open set in
be an arbitrary open set in 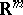 (in particular,
(in particular,  ), let
), let  be a unit vector in
be a unit vector in 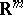 , let
, let 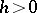 and let
and let  be the set of points
be the set of points 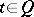 such that the segment
such that the segment  . If
. If 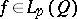 and
and 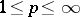 , then the quantity
, then the quantity
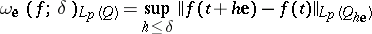 |
is called the modulus of continuity of the function 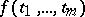 in the direction
in the direction  with respect to the metric of
with respect to the metric of 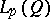 . The quantity
. The quantity
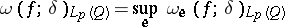 |
is called the modulus of continuity of 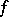 in
in 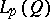 .
.
In the periodic case, the best approximation 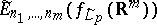 of a function
of a function 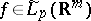 having (Sobolev generalized) partial derivatives
having (Sobolev generalized) partial derivatives
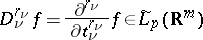 |
(where the 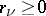 are integers and
are integers and 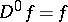 ,
, 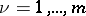 ) by trigonometric polynomials
) by trigonometric polynomials 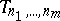 , satisfies the inequality
, satisfies the inequality
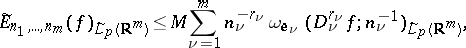 | (3) |
where 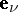 is the unit vector directed along
is the unit vector directed along 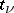 , and where the constant
, and where the constant 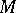 depends neither on
depends neither on 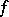 nor on
nor on 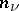 . For a function
. For a function 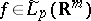 having generalized partial derivatives
having generalized partial derivatives
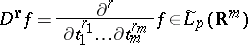 |
of order 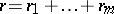 (where
(where 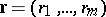 ), the following inequalities hold:
), the following inequalities hold:
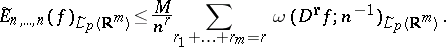 | (4) |
If
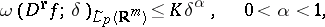 |
i.e. if the function 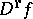 satisfies a Hölder condition, then
satisfies a Hölder condition, then
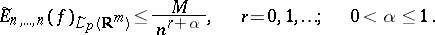 | (5) |
In the last case the inverse theorem asserts that if for a function 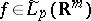 inequality (5) holds for all
inequality (5) holds for all 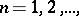 then the derivatives
then the derivatives 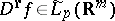 exist and satisfy for any
exist and satisfy for any  the inequalities
the inequalities
 | (6) |
for 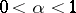 ; whereas
; whereas
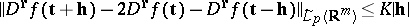 | (7) |
for 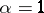 . Here
. Here 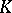 does not depend on the length
does not depend on the length 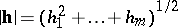 of the vector
of the vector 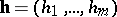 .
.
Theorems analogous to those given above also hold for non-periodic functions 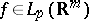 if entire functions of exponential type are used as tools of approximation. The above-mentioned results can be extended also to classes of functions whose smoothness is described in terms of moduli of continuity (moduli of smoothness) of a higher order (see [1]).
if entire functions of exponential type are used as tools of approximation. The above-mentioned results can be extended also to classes of functions whose smoothness is described in terms of moduli of continuity (moduli of smoothness) of a higher order (see [1]).
In the case of approximating functions 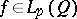 by algebraic polynomials
by algebraic polynomials  on a bounded parallelepiped (as well on some other bounded sets) direct theorems similar to (3), (4) and (5) have been proved. Inverses of these theorems, like in the case of functions defined on a bounded interval, are possible only on a proper subset
on a bounded parallelepiped (as well on some other bounded sets) direct theorems similar to (3), (4) and (5) have been proved. Inverses of these theorems, like in the case of functions defined on a bounded interval, are possible only on a proper subset 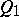 of
of 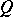 . Inverse theorems are known assuming a better order of approximation in the neighbourhood of boundary of
. Inverse theorems are known assuming a better order of approximation in the neighbourhood of boundary of 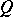 (see [13]); there are also direct theorems asserting the possibility of achieving such an improvement in a neighbourhood of angular points (see [14]). Necessary and sufficient conditions for a function
(see [13]); there are also direct theorems asserting the possibility of achieving such an improvement in a neighbourhood of angular points (see [14]). Necessary and sufficient conditions for a function 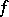 to belong to a class
to belong to a class 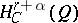 (defined in the metric of
(defined in the metric of 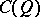 ) by conditions similar to the conditions (6) and (7)) at the cost of raising the order of approximation in a neighbourhood of the boundary (like in the one-dimensional case) are unknown (1983). However, one has the following results of a negative character (see [13]). Let
) by conditions similar to the conditions (6) and (7)) at the cost of raising the order of approximation in a neighbourhood of the boundary (like in the one-dimensional case) are unknown (1983). However, one has the following results of a negative character (see [13]). Let 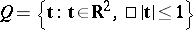 . There does not exist a sequence
. There does not exist a sequence 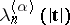 ,
, 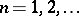 ;
; 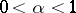 , of functions in
, of functions in 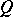 having the two following properties:
having the two following properties:
1) For any function 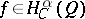 there are a constant
there are a constant 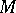 and a sequence of polynomials
and a sequence of polynomials
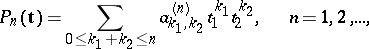 |
such that
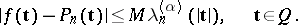 | (8) |
2) The existence of a constant  and of a sequence of polynomials
and of a sequence of polynomials 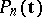 satisfying (8) implies that
satisfying (8) implies that 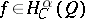 for any function
for any function 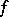 defined on
defined on 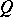 .
.
To illustrate the specific nature of approximation of functions of several variables, one can mention the following results.
Let 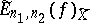 be the best approximation of a
be the best approximation of a 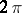 -periodic function
-periodic function 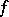 of two variables by trigonometric polynomials
of two variables by trigonometric polynomials 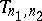 in the metric of
in the metric of 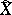 (
(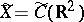 or
or 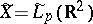 ), and let
), and let 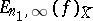 be the best approximation of
be the best approximation of 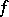 in
in 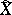 by functions
by functions 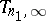 , i.e. by trigonometric polynomials of degree at most
, i.e. by trigonometric polynomials of degree at most 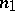 in the variable
in the variable 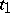 and with coefficients that are functions of
and with coefficients that are functions of 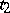 . The quantity
. The quantity 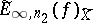 is defined similarly.
is defined similarly.
If 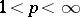 , one has the inequalities
, one has the inequalities
 |
where 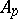 depends only on
depends only on 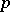 .
.
If 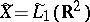 or
or 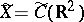 , then
, then
 | (9) |
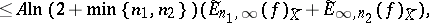 |
where 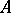 is an absolute constant, and the factor
is an absolute constant, and the factor 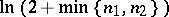 in (9) cannot be replaced by another factor tending slower to infinity as
in (9) cannot be replaced by another factor tending slower to infinity as 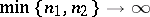 (see [15]).
(see [15]).
Fundamental peculiarities arise in problems of interpolation for functions of several variables. For instance, contrary to the one-dimensional case, the existence of an algebraic interpolation polynomial depends substantially on the position of the interpolation nodes. Nevertheless, effective methods of constructing polynomials and splines interpolating a function 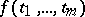 on a distribution of nodes chosen in a definite way, have been established (see Interpolation). For multi-dimensional interpolation by splines, in a number of cases order estimates of the approximation errors, for the function
on a distribution of nodes chosen in a definite way, have been established (see Interpolation). For multi-dimensional interpolation by splines, in a number of cases order estimates of the approximation errors, for the function 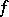 as well as for its partial derivatives, have been found; in this direction, two-dimensional splines of low degree, as well as local (Hermitian) splines of arbitrary degree, have been studied in more detail (see [7], [10]–[12]). Among the other linear methods for approximating functions of several variables, multiple Fourier sums and their various means have been studied most extensively. Here, order estimates of the approximation with respect to classes of functions are known, and in some case asymptotically exact results were obtained (see [5], [6] and [8]).
as well as for its partial derivatives, have been found; in this direction, two-dimensional splines of low degree, as well as local (Hermitian) splines of arbitrary degree, have been studied in more detail (see [7], [10]–[12]). Among the other linear methods for approximating functions of several variables, multiple Fourier sums and their various means have been studied most extensively. Here, order estimates of the approximation with respect to classes of functions are known, and in some case asymptotically exact results were obtained (see [5], [6] and [8]).
References
| [1] | S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian) |
| [2] | R.S. Guter, L.D. Kudryavtsev, B.M. Levitan, "Elements of the theory of functions" , Moscow (1963) pp. 106–198 (In Russian) |
| [3] | N.P. Korneichuk, "Extremal problems in approximation theory" , Moscow (1976) (In Russian) |
| [4] | V.M. Tikhomirov, "Some problems in approximation theory" , Moscow (1976) (In Russian) |
| [5] | V.K. Dzyadyk, "Introduction to the theory of uniform approximation of functions by polynomials" , Moscow (1977) (In Russian) |
| [6] | A.F. Timan, "Theory of approximation of functions of a real variable" , Pergamon (1963) (Translated from Russian) |
| [7] | S.B. Stechkin, Yu.N. Subbotin, "Splines in numerical mathematics" , Moscow (1976) (In Russian) |
| [8] | A.I. Stepanets, "Uniform approximation by trigonometric polynomials. Linear methods" , Kiev (1980) (In Russian) |
| [9] | P.J. Laurent, "Approximation et optimisation" , Hermann (1972) |
| [10] | J.H. Ahlberg, E.N. Nilson, J.F. Walsh, "Theory of splines and their applications" , Acad. Press (1967) |
| [11] | V.L. Miroshichenko, "Methods of spline functions" , Moscow (1980) |
| [12] | R.S. Varga, "Functional analysis and approximation theory in numerical analysis" , Reg. Conf. Ser. Appl. Math. , 3 , SIAM (1971) |
| [13] | S.M. Nikol'skii, "Approximation of functions of several variables by polynomials" Siberian Math. J. , 10 : 4 (1969) pp. 792–799 Sibirsk. Mat. Zh. , 10 (1969) pp. 1075–1083 |
| [14] | Yu.A. Brudnyi, "Approximation of functions defined in a convex polyhedron" Soviet Math. Doklady , 11 : 6 (1970) pp. 1587–1590 Dokl. Akad. Nauk SSSR , 195 (1970) pp. 1007–1009 |
| [15] | V.N. Teml'yakov, "Best approximations for functions of two variables" Soviet Math. Doklady , 16 : 4 (1975) pp. 1051–1055 Dokl. Akad. Nauk SSSR , 223 (1975) pp. 1079–1082 |
Comments
References
| [a1] | E.W. Cheney, "Four lectures on multivariate approximation" S.P. Singh (ed.) J.H.W. Burry (ed.) B. Watson (ed.) , Approximation theory and spline functions , Reidel (1984) pp. 65–87 |
| [a2] | W. Schempp (ed.) K. Zeller (ed.) , Multivariate approximation theory , Birkhäuser (1979) |
| [a3] | W. Schempp (ed.) K. Zeller (ed.) , Multivariate approximation theory , II , Birkhäuser (1982) |
| [a4] | W. Schempp (ed.) K. Zeller (ed.) , Multivariate approximation theory , III , Birkhäuser (1985) |
| [a5] | W. Schempp (ed.) K. Zeller (ed.) , Constructive theory of functions of several variables , Springer (1977) |
| [a6] | G.G. Lorentz, "Approximation of functions" , Holt, Rinehart & Winston (1966) |
| [a7] | M. Golomb, "Approximation by functions of fewer variables" R.E. Langer (ed.) , On numerical approximation , Univ. of Wisconsin Press (1959) pp. 275–327 |
| [a8] | L.L. Schumaker, "Spline functions, basic theory" , Wiley (1981) |
Approximation of functions of several real variables. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Approximation_of_functions_of_several_real_variables&oldid=12943