Approximation of functions, measure of

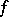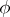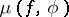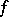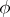A quantitative expression for the error of an approximation. When the discussion is about the approximation of a function by a function , the measure of approximation is usually defined by the metric in a function space containing both and . For example, if 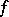and 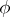are continuous functions on a segment 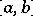, the uniform metric of 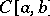is commonly used, i.e. one puts

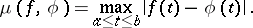If continuity of the approximated function is not guaranteed or if the conditions of the problem imply that it is important that and 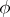are close on 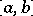in an average sense, the integral metric of a space may be used, putting

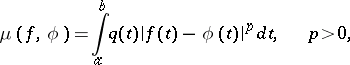where 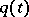is a weight function. The case 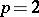is most often used and is most convenient from a practical point of view (cf. Mean-square approximation of a function).

The measure of approximation may take into account only values of 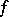and 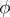in discrete points , , 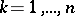of , e.g.

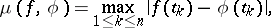where 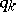are certain positive coefficients.

One defines in an analogous way the measure of approximation of functions in two or more variables.

The measure of approximation of a function by a family 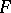of functions is usually taken to be the best approximation:

The quantity

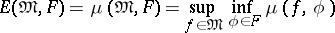is usually taken as the measure of approximation of a class of functions 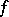by functions 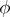from a certain fixed set 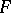. It characterizes the maximal deviation of functions in 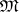from functions in 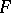that are closest to them.

In general, when approximation in an arbitrary metric space 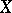is considered, the measure of approximation 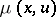of an element by an element (a set 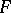) is the distance 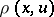(or 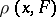) between and (or 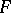) in the metric of .

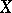References

[1]	V.L. Goncharov, "The theory of interpolation and approximation of functions" , Moscow (1954) (In Russian)
[2]	S.M. Nikol'skii, "Approximation of functions of several variables and imbedding theorems" , Springer (1975) (Translated from Russian)
[3]	J.R. Rice, "The approximation of functions" , 1–2 , Addison-Wesley (1964–1968)

Comments

The measure of approximation is also called the error measure.

References

[a1]	G.G. Lorentz, "Approximation of functions" , Holt, Rinehart & Winston (1966)
[a2]	A. Pinkus, "-widths in approximation theory" , Springer (1985) (Translated from Russian)