Approximation of a differential equation by difference equations
An approximation of a differential equation by a system of algebraic equations for the values of the unknown functions on some grid, which is made more exact by making the parameter (mesh, step) of the grid tend to zero.
Let 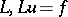 , be some differential operator and let
, be some differential operator and let  , be some finite-difference operator (cf. Approximation of a differential operator by difference operators). One says that the finite-difference expression
, be some finite-difference operator (cf. Approximation of a differential operator by difference operators). One says that the finite-difference expression 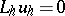 ,
,  , is an approximation of order
, is an approximation of order 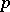 to the differential equation
to the differential equation 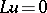 on solutions
on solutions  if the operator
if the operator  approximates the operator
approximates the operator 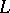 on solutions
on solutions  of order
of order 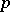 , i.e. if
, i.e. if
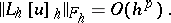 |
The simplest example of the construction of a finite-difference equation 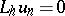 which approximates the differential equation
which approximates the differential equation 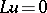 on solutions
on solutions  , consists in replacing each derivative in the expression
, consists in replacing each derivative in the expression 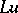 by its finite-difference analogue.
by its finite-difference analogue.
For instance, the equation
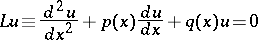 |
is approximated with second-order accuracy by the finite-difference equation
 |
 |
where the grids  and
and 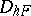 consist of points
consist of points  ,
, 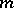 is an integer, and
is an integer, and 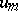 is the value of the function
is the value of the function  at
at 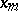 . Again, the equation
. Again, the equation
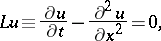 |
is approximated by two different difference approximations on smooth solutions:
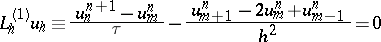 |
(explicit scheme), and
 |
(implicit scheme), in which the grids  and
and  consist of the points
consist of the points 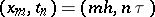 ,
,  ,
, 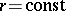 ,
, 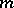 and
and  are integers, and
are integers, and 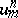 is the value of the function
is the value of the function 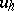 at the point
at the point 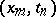 of the grid. There exist finite-difference operators
of the grid. There exist finite-difference operators 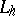 which represent an approximation to the differential operator
which represent an approximation to the differential operator 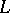 especially well only on solutions
especially well only on solutions  of the equation
of the equation  and less well on other functions. For instance, the operator
and less well on other functions. For instance, the operator 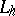 ,
,
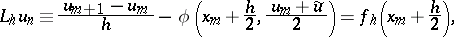 |
where 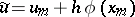 , is a first-order approximation (with respect to
, is a first-order approximation (with respect to 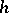 ) of the operator
) of the operator 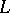 ,
,
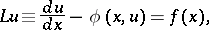 |
on arbitrary smooth functions 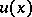 and it is a second-order approximation on solutions of the equation
and it is a second-order approximation on solutions of the equation  (it is assumed that the function
(it is assumed that the function  is sufficiently smooth). When finding numerical solutions of boundary value problems for the differential equation
is sufficiently smooth). When finding numerical solutions of boundary value problems for the differential equation  with the aid of the finite-difference equation
with the aid of the finite-difference equation  , it is the approximation property of
, it is the approximation property of  when applied to solutions
when applied to solutions  of
of 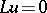 that is significant and not its approximation property when applied to arbitrary smooth functions. For a large class of differential equations and systems of equations there exist methods for constructing difference equations approximating them, which also meet various additional conditions: stability of the solution
that is significant and not its approximation property when applied to arbitrary smooth functions. For a large class of differential equations and systems of equations there exist methods for constructing difference equations approximating them, which also meet various additional conditions: stability of the solution  with respect to rounding-off errors such as are permitted in the calculations; the validity of certain integral relations for
with respect to rounding-off errors such as are permitted in the calculations; the validity of certain integral relations for  which hold for the solution
which hold for the solution  of the differential equation; the permissibility of using arbitrary grids
of the differential equation; the permissibility of using arbitrary grids  and
and 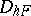 (this is important in calculating the motion of a continuous medium); a limitation on the number of arithmetical operations required to compute the solutions; etc.
(this is important in calculating the motion of a continuous medium); a limitation on the number of arithmetical operations required to compute the solutions; etc.
The approximation of a differential equation by difference equations is an element of the approximation of a differential boundary value problem by difference boundary value problems in order to approximately calculate a solution of the former.
References
| [1] | S.K. Godunov, V.S. Ryaben'kii, "The theory of difference schemes" , North-Holland (1964) (Translated from Russian) |
| [2] | A.A. Samarskii, "Theorie der Differenzverfahren" , Akad. Verlagsgesell. Geest u. Portig K.-D. (1984) (Translated from Russian) |
| [3] | S.K. Godunov, et al., "Numerical solution of multi-dimensional problems of gas dynamics" , Moscow (1976) (In Russian) |
| [4] | A.A. Samarskii, Yu.P. Popov, "Difference schemes of gas dynamics" , Moscow (1975) (In Russian) |
Comments
For additional references, see the additional references to Approximation of a differential operator by difference operators.
Approximation of a differential equation by difference equations. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Approximation_of_a_differential_equation_by_difference_equations&oldid=12012