Approximately-compact set
From Encyclopedia of Mathematics
A set having the property of approximate compactness. A metric projection on any approximately-compact Chebyshev set is continuous. Examples of approximately-compact sets include boundedly-compact sets and closed convex sets in the spaces 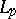 (
(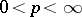 ), and the set of rational fractions in which the degrees of the numerator and denominator are constant. In approximation theory and in the theory of ill-posed problems frequent use is made of spaces in which all closed sets are approximately compact.
), and the set of rational fractions in which the degrees of the numerator and denominator are constant. In approximation theory and in the theory of ill-posed problems frequent use is made of spaces in which all closed sets are approximately compact.
References
| [1] | N.V. Efimov, S.B. Stechkin, "Approximative compactness and Čebyšev sets" Soviet Math. Dokl. , 2 : 5 (1961) pp. 1226–1228 Dokl. Akad. Nauk SSSR , 140 : 3 (1961) pp. 522–524 |
| [2] | L.P. Vlasov, "Approximative properties of sets in normed linear spaces" Russian Math. Surveys , 28 : 6 (1973) pp. 1–66 Uspekhi Mat. Nauk , 28 : 6 (1973) pp. 3–66 |
How to Cite This Entry:
Approximately-compact set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Approximately-compact_set&oldid=15348
Approximately-compact set. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Approximately-compact_set&oldid=15348
This article was adapted from an original article by Yu.N. Subbotin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article