Approximate differentiability

A generalization of the concept of differentiability obtained by replacing the ordinary limit by an approximate limit. A real-valued function of a real variable is called approximately differentiable at a point if there exists a number such that

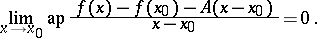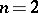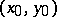The magnitude is called the approximate differential of at . A function is approximately differentiable at a point if and only if it has an approximate derivative at this point. Approximate differentiability of real functions of real variables is defined in a similar manner. For example, for , is called approximately differentiable at a point if

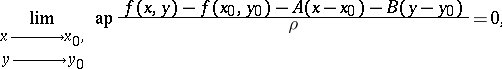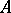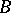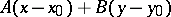where and are certain given numbers and . The expression is called the approximate differential of at .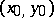

Stepanov's theorem: A real-valued measurable function 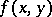on a set 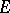is approximately differentiable almost-everywhere on 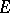if and only if it has finite approximate partial derivatives with respect to and to almost-everywhere on 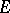; these partial derivatives almost-everywhere on 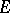coincide with the coefficients 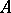and 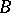, respectively, of the approximate differential.

The concept of approximate differentiability can also be extended to vector functions of one or more real variables.

References

[1]	S. Saks, "Theory of the integral" , Hafner (1952) (Translated from French)

Comments

For other references see Approximate limit.