Approximate compactness
A property of a set 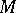 in a metric space
in a metric space 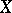 requiring that for any
requiring that for any 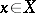 , every minimizing sequence
, every minimizing sequence 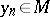 (i.e. a sequence with the property
(i.e. a sequence with the property 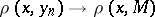 ) has a limit point
) has a limit point 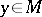 . Approximate compactness of a given set ensures the existence of an element of best approximation for any
. Approximate compactness of a given set ensures the existence of an element of best approximation for any 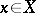 . The concept of approximate compactness was introduced [1] in connection with the study of Chebyshev sets (cf. Chebyshev set) in a Banach space, which made it possible to describe convex Chebyshev sets in certain spaces. In fact, let
. The concept of approximate compactness was introduced [1] in connection with the study of Chebyshev sets (cf. Chebyshev set) in a Banach space, which made it possible to describe convex Chebyshev sets in certain spaces. In fact, let 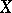 be a uniformly-convex smooth Banach space. For a Chebyshev set
be a uniformly-convex smooth Banach space. For a Chebyshev set 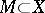 to be convex, it is necessary and sufficient that it be approximately compact. It follows, in particular, that the set of rational fractions with fixed degrees of the numerator and the denominator is not a Chebyshev set in the space
to be convex, it is necessary and sufficient that it be approximately compact. It follows, in particular, that the set of rational fractions with fixed degrees of the numerator and the denominator is not a Chebyshev set in the space 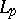 (
(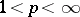 ) if the degree of the denominator is not smaller than one [1].
) if the degree of the denominator is not smaller than one [1].
For subsequent studies on this subject see [2].
References
| [1] | N.V. Efimov, S.B. Stechkin, "Approximative compactness and Čebyšev sets" Soviet Math. Dokl. , 2 : 5 (1961) pp. 522–524 Dokl. Akad. Nauk SSSR , 140 : 3 (1961) pp. 522–524 |
| [2] | A.L. Garkavi, "The theory of best approximation in normed linear spaces" Itogi Nauk. Mat. Anal. 1967 (1969) pp. 75–132 (In Russian) |
Approximate compactness. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Approximate_compactness&oldid=15388