Anti-parallel straight lines
with respect to two given lines $m_1$ and $m_2$
Two straight lines $l_1$ and $l_2$ which intersect $m_1$ and $m_2$ so that $\angle1=\angle2$ (cf. Fig.).
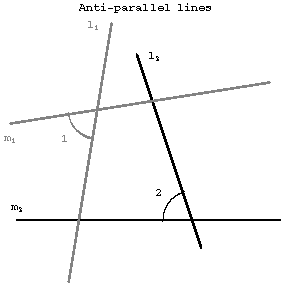
Figure: a012660a
If $l_1$ and $l_2$ are anti-parallel with respect to $m_1$ and $m_2$, then $m_1$ and $m_2$ are also anti-parallel with respect to $l_1$ and $l_2$. In any quadrilateral inscribed in a circle, any two opposite sides are anti-parallel with respect to the other two sides. If the lines $m_1$ and $m_2$ intersect at a point $O$, one also says that $l_1$ and $l_2$ are anti-parallel with respect to the angle $m_1Om_2$. If the lines $m_1$ and $m_2$ coincide, $l_1$ and $l_2$ are said to be anti-parallel with respect to a straight line.
Anti-parallel straight lines. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Anti-parallel_straight_lines&oldid=31542