Anti-eigenvalue

The theory of anti-eigenvalues is a spectral theory based upon the turning angles of a matrix or operator . (See Eigen value for the spectral theory of stretchings, rather than turnings, of a matrix or operator.)

For a strongly accretive operator , i.e., , , 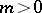the first anti-eigenvalue is defined by

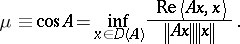(a1)

From (a1) one has immediately the notion of the angle : the largest angle through which may turn a vector. Any corresponding vector which is turned by that angle is called a first anti-eigenvector. It turns out that, in general, the first anti-eigenvectors come in pairs. Two important early results were the minmax theorem and the Euler equation.

Minmax theorem.

For any strongly accretive bounded operator on a Hilbert space ,

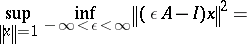(a2)

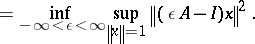Using the minmax theorem, the right-hand side of (a2) is seen to define

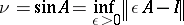(a3)

in such a way that 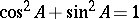. This implies an operator trigonometry (see [a1]).

Euler equation.

For any strongly accretive bounded operator 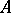on a Hilbert space 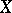, the Euler equation for the anti-eigenvalue functional 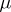in (a1) is

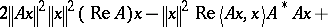(a4)

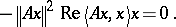When 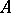is a normal operator, (a4) is satisfied not only by the first anti-eigenvectors of 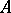, but by all eigenvectors of . Therefore the Euler equation may be viewed as a significant extension of the Rayleigh–Ritz theory for the variational characterization of eigenvalues of a self-adjoint or normal operator 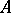. The eigenvectors maximize the variational quotient (a1). The anti-eigenvectors minimize it. See [a2], [a3].

The theory of anti-eigenvalues has been applied recently (from 1990 onward) to gradient and iterative methods for the solution of linear systems 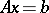; see [a5], [a6]. For example, the Kantorovich convergence rate for steepest descent,

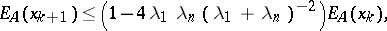where 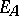denotes the 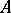-inner-product error 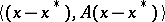, becomes

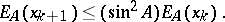Thus, the Kantorovich error rate is trigonometric. Similar trigonometric convergence bounds hold for conjugate gradient and related more sophisticated algorithms [a4]. Even the basic Richardson method 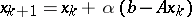(cf. also Richardson extrapolation) may be seen to have optimal convergence rate 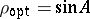. For further information, see [a5], [a6].

References

[a1]	K. Gustafson, "Operator trigonometry" Linear Multilinear Alg. , 37 (1994) pp. 139–159
[a2]	K. Gustafson, "Antieigenvalues" Linear Alg. & Its Appl. , 208/209 (1994) pp. 437–454
[a3]	K. Gustafson, "Matrix trigonometry" Linear Alg. & Its Appl. , 217 (1995) pp. 117–140
[a4]	K. Gustafson, "Operator trigonometry of iterative methods" Numerical Linear Alg. Appl. , to appear (1997)
[a5]	K. Gustafson, "Lectures on computational fluid dynamics, mathematical physics, and linear algebra" , Kaigai & World Sci. (1996/7)
[a6]	K. Gustafson, D. Rao, "Numerical range" , Springer (1997)