Anti-Lie triple system
A triple system is a vector space  over a field
over a field  together with a
together with a  -trilinear mapping
-trilinear mapping  . A triple system
. A triple system  satisfying
satisfying
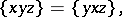 | (a1) |
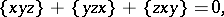 | (a2) |
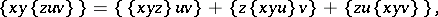 | (a3) |
for all  , is called an anti-Lie triple system.
, is called an anti-Lie triple system.
If instead of (a1) one has 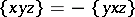 , a Lie triple system is obtained.
, a Lie triple system is obtained.
Assume that 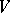 is an anti-Lie triple system and that
is an anti-Lie triple system and that 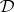 is the Lie algebra of derivations of
is the Lie algebra of derivations of  containing the inner derivation
containing the inner derivation 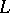 defined by
defined by  . Consider
. Consider  with
with 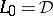 and
and 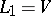 , and with product given by
, and with product given by 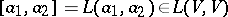 ,
, 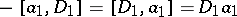 ,
, 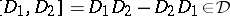 for
for  ,
, 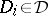 (
(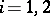 ). Then the definition of anti-Lie triple system implies that
). Then the definition of anti-Lie triple system implies that 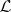 is a Lie superalgebra (cf. also Lie algebra). Hence
is a Lie superalgebra (cf. also Lie algebra). Hence 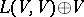 is an ideal of the Lie superalgebra
is an ideal of the Lie superalgebra 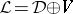 . One denotes
. One denotes 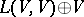 by
by 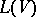 and calls it the standard embedding Lie superalgebra of
and calls it the standard embedding Lie superalgebra of 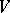 . This concept is useful to obtain a construction of Lie superalgebras as well as a construction of Lie algebras from Lie triple systems.
. This concept is useful to obtain a construction of Lie superalgebras as well as a construction of Lie algebras from Lie triple systems.
References
| [a1] | J.R. Faulkner, J.C. Ferrar, "Simple anti-Jordan pairs" Commun. Algebra , 8 (1980) pp. 993–1013 |
| [a2] | N. Kamiya, "A construction of anti-Lie triple systems from a class of triple systems" Memoirs Fac. Sci. Shimane Univ. , 22 (1988) pp. 51–62 |
Anti-Lie triple system. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Anti-Lie_triple_system&oldid=16792