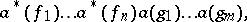A family of closed linear operators 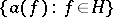 , where
, where  is some Hilbert space, acting on a Fock space constructed from
is some Hilbert space, acting on a Fock space constructed from  (i.e. on the symmetrization
(i.e. on the symmetrization 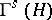 or anti-symmetrization
or anti-symmetrization 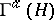 of the space of tensors over
of the space of tensors over  ) such that on the vector
) such that on the vector 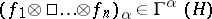 ,
, 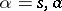 , consisting of the symmetrized
, consisting of the symmetrized 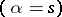 or anti-symmetrized
or anti-symmetrized  tensor product of a sequence of elements
tensor product of a sequence of elements 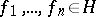 ,
, 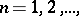 in
in 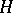 , they are given by the formulas:
, they are given by the formulas:
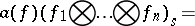 | (1) |
in the symmetric case, and
 | (2) |
in the anti-symmetric case; the empty vector  ,
, 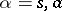 (i.e. the unit vector in the subspace of constants in
(i.e. the unit vector in the subspace of constants in 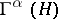 ) is mapped to zero by
) is mapped to zero by  . In these formulas
. In these formulas 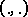 is the inner product in
is the inner product in  . The operators
. The operators 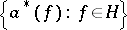 dual to the operators
dual to the operators 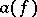 are called creation operators; their action on the vectors
are called creation operators; their action on the vectors 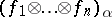 ,
, 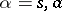 ,
, 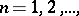 is given by the formulas
is given by the formulas
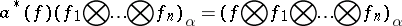 | (3) |
and
As a consequence of these definitions, for each 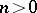 the subspace
the subspace 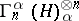 ,
, 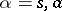 , the symmetrized or anti-symmetrized
, the symmetrized or anti-symmetrized  -th tensor power of
-th tensor power of 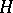 , is mapped by
, is mapped by  into
into 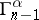 and by
and by 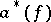 into
into 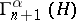 .
.
In quantum physics, the Fock space 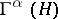 ,
,  , is interpreted as the state space of a system consisting of an arbitrary (finite) number of identical quantum particles, the space
, is interpreted as the state space of a system consisting of an arbitrary (finite) number of identical quantum particles, the space 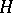 is the state space of a single particle, the subspace
is the state space of a single particle, the subspace 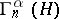 corresponds to the states of the system with
corresponds to the states of the system with  particles, i.e. states in which there are just
particles, i.e. states in which there are just  particles. A state with
particles. A state with  particles is mapped by
particles is mapped by 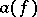 to a state with
to a state with 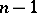 particles ( "annihilation" of a particle), and by
particles ( "annihilation" of a particle), and by 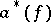 to a state with
to a state with 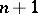 particles ( "creation" of a particle).
particles ( "creation" of a particle).
The operators 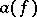 and
and  form irreducible families of operators satisfying the following permutation relations: In the symmetric case (the commutation relations)
form irreducible families of operators satisfying the following permutation relations: In the symmetric case (the commutation relations)
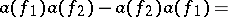 | (4) |
and in the anti-symmetric case (the anti-commutation relations)
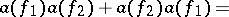 | (5) |
where 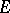 is the identity operator in
is the identity operator in 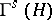 or
or 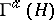 . Besides the families of operators
. Besides the families of operators 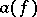 and
and  ,
,  , described here, there exist in the case of an infinite-dimensional space
, described here, there exist in the case of an infinite-dimensional space 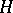 also other irreducible representations of the commutation and anti-commutation relations (4) and (5), not equivalent to those given above. Sometimes they are also called creation and annihilation operators. In the case of a finite-dimensional space
also other irreducible representations of the commutation and anti-commutation relations (4) and (5), not equivalent to those given above. Sometimes they are also called creation and annihilation operators. In the case of a finite-dimensional space 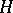 , all irreducible representations of the commutation or anti-commutation relations are unitarily equivalent.
, all irreducible representations of the commutation or anti-commutation relations are unitarily equivalent.
The operators 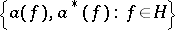 are in many connections convenient "generators" in the set of all linear operators acting in the space
are in many connections convenient "generators" in the set of all linear operators acting in the space 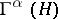 ,
, 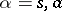 , and the representation of such operators as the sum of arbitrary creation and annihilation operators (the normal form of an operator) is very useful in applications. The connection with this formalism bears the name method of second quantization, cf. [1].
, and the representation of such operators as the sum of arbitrary creation and annihilation operators (the normal form of an operator) is very useful in applications. The connection with this formalism bears the name method of second quantization, cf. [1].
In the particular, but for applications important, case in which 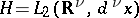 ,
, 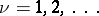 (or in a more general case
(or in a more general case 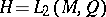 , where
, where 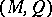 is a measure space), the family of operators
is a measure space), the family of operators 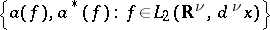 defines two operator-valued generalized functions
defines two operator-valued generalized functions 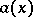 and
and 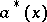 such that
such that
The introduction of  and
and 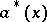 turns out to be convenient for the formalism of second quantization (e.g. it allows one directly to consider operators of the form
turns out to be convenient for the formalism of second quantization (e.g. it allows one directly to consider operators of the form
where 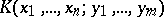 is a certain "sufficiently-good" function), without having to recourse to their decomposition as a series in the monomials
is a certain "sufficiently-good" function), without having to recourse to their decomposition as a series in the monomials
where
References
| [1] | F.A. Berezin, "The method of second quantization" , Acad. Press (1966) (Translated from Russian) (Revised (augmented) second edition: Kluwer, 1989) |
| [2] | R.L. Dobrushin, R.A. Minlos, Uspekhi Mat. Nauk , 32 : 2 (1977) pp. 67–122 |
| [3] | L. Gårding, A. Wightman, Proc. Nat. Acad. Sci. U.S.A. , 40 : 7 (1954) pp. 617–626 |
References
| [a1] | J. Glimm, A. Jaffe, "Quantum physics, a functional integral point of view" , Springer (1981) |
| [a2] | N.N. Bogolyubov, A.A. Logunov, I.T. Todorov, "Introduction to axiomatic quantum field theory" , Benjamin (1975) (Translated from Russian) |
| [a3] | J. de Boer, "Construction operator formalism in many particle systems" J. de Boer (ed.) G.E. Uhlenbeck (ed.) , Studies in statistical mechanics , North-Holland (1965) |
How to Cite This Entry:
Annihilation operators. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Annihilation_operators&oldid=15988
This article was adapted from an original article by R.A. Minlos (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article , where
, where 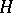 is some Hilbert space, acting on a Fock space constructed from
is some Hilbert space, acting on a Fock space constructed from 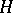 (i.e. on the symmetrization
(i.e. on the symmetrization 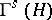 or anti-symmetrization
or anti-symmetrization 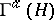 of the space of tensors over
of the space of tensors over  ) such that on the vector
) such that on the vector 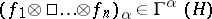 ,
, 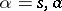 , consisting of the symmetrized
, consisting of the symmetrized 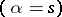 or anti-symmetrized
or anti-symmetrized  tensor product of a sequence of elements
tensor product of a sequence of elements 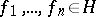 ,
, 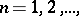 in
in 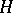 , they are given by the formulas:
, they are given by the formulas:
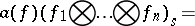
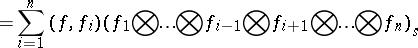

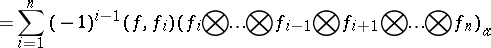
 ,
, 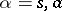 (i.e. the unit vector in the subspace of constants in
(i.e. the unit vector in the subspace of constants in 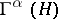 ) is mapped to zero by
) is mapped to zero by  . In these formulas
. In these formulas 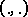 is the inner product in
is the inner product in  . The operators
. The operators 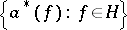 dual to the operators
dual to the operators 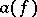 are called creation operators; their action on the vectors
are called creation operators; their action on the vectors 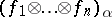 ,
, 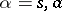 ,
, 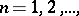 is given by the formulas
is given by the formulas
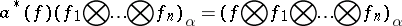

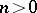 the subspace
the subspace 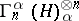 ,
, 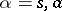 , the symmetrized or anti-symmetrized
, the symmetrized or anti-symmetrized  -th tensor power of
-th tensor power of 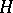 , is mapped by
, is mapped by  into
into 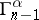 and by
and by 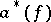 into
into 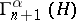 .
.
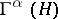 ,
,  , is interpreted as the state space of a system consisting of an arbitrary (finite) number of identical quantum particles, the space
, is interpreted as the state space of a system consisting of an arbitrary (finite) number of identical quantum particles, the space 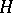 is the state space of a single particle, the subspace
is the state space of a single particle, the subspace 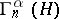 corresponds to the states of the system with
corresponds to the states of the system with  particles, i.e. states in which there are just
particles, i.e. states in which there are just  particles. A state with
particles. A state with  particles is mapped by
particles is mapped by 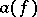 to a state with
to a state with 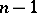 particles ( "annihilation" of a particle), and by
particles ( "annihilation" of a particle), and by 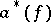 to a state with
to a state with 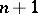 particles ( "creation" of a particle).
particles ( "creation" of a particle).
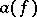 and
and  form irreducible families of operators satisfying the following permutation relations: In the symmetric case (the commutation relations)
form irreducible families of operators satisfying the following permutation relations: In the symmetric case (the commutation relations)
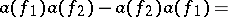

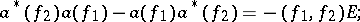
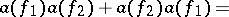
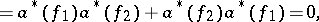
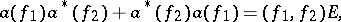
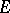 is the identity operator in
is the identity operator in 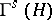 or
or 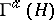 . Besides the families of operators
. Besides the families of operators 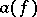 and
and  ,
,  , described here, there exist in the case of an infinite-dimensional space
, described here, there exist in the case of an infinite-dimensional space 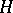 also other irreducible representations of the commutation and anti-commutation relations (4) and (5), not equivalent to those given above. Sometimes they are also called creation and annihilation operators. In the case of a finite-dimensional space
also other irreducible representations of the commutation and anti-commutation relations (4) and (5), not equivalent to those given above. Sometimes they are also called creation and annihilation operators. In the case of a finite-dimensional space 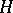 , all irreducible representations of the commutation or anti-commutation relations are unitarily equivalent.
, all irreducible representations of the commutation or anti-commutation relations are unitarily equivalent.
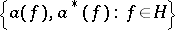 are in many connections convenient "generators" in the set of all linear operators acting in the space
are in many connections convenient "generators" in the set of all linear operators acting in the space 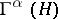 ,
, 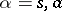 , and the representation of such operators as the sum of arbitrary creation and annihilation operators (the normal form of an operator) is very useful in applications. The connection with this formalism bears the name method of second quantization, cf. [1].
, and the representation of such operators as the sum of arbitrary creation and annihilation operators (the normal form of an operator) is very useful in applications. The connection with this formalism bears the name method of second quantization, cf. [1].
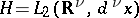 ,
, 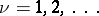 (or in a more general case
(or in a more general case 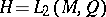 , where
, where 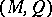 is a measure space), the family of operators
is a measure space), the family of operators 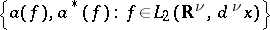 defines two operator-valued generalized functions
defines two operator-valued generalized functions 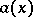 and
and 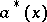 such that
such that

 and
and 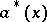 turns out to be convenient for the formalism of second quantization (e.g. it allows one directly to consider operators of the form
turns out to be convenient for the formalism of second quantization (e.g. it allows one directly to consider operators of the form
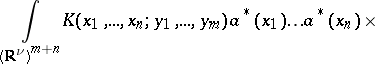
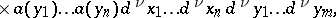
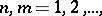
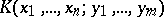 is a certain "sufficiently-good" function), without having to recourse to their decomposition as a series in the monomials
is a certain "sufficiently-good" function), without having to recourse to their decomposition as a series in the monomials