Angular boundary value
From Encyclopedia of Mathematics
boundary value along a non-tangential path
The value associated to a complex function  defined in the unit disc
defined in the unit disc  at a boundary point
at a boundary point  , equal to the limit
, equal to the limit
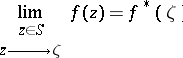 |
of  on the set of points of the angular domain
on the set of points of the angular domain
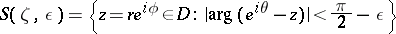 |
under the condition that this limit exists for all  ,
,  , and hence does not depend on
, and hence does not depend on  . The term is sometimes applied in a more general sense to functions
. The term is sometimes applied in a more general sense to functions  given in an arbitrary (including a higher-dimensional) domain
given in an arbitrary (including a higher-dimensional) domain 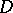 ; for
; for  one takes the intersection with
one takes the intersection with  of an angular (or conical) domain with vertex
of an angular (or conical) domain with vertex  , with axis normal to the boundary
, with axis normal to the boundary 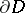 at
at 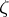 and with angle
and with angle 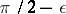 ,
,  .
.
References
| [1] | A.I. Markushevich, "Theory of functions of a complex variable" , 1–2 , Chelsea (1977) (Translated from Russian) |
| [2] | I.I. [I.I. Privalov] Priwalow, "Randeigenschaften analytischer Funktionen" , Deutsch. Verlag Wissenschaft. (1956) (Translated from Russian) |
Comments
An angular boundary value is also called a non-tangential boundary value. Cf. Boundary properties of analytic functions.
How to Cite This Entry:
Angular boundary value. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Angular_boundary_value&oldid=12519
Angular boundary value. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Angular_boundary_value&oldid=12519
This article was adapted from an original article by E.D. Solomentsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article