Anger function
From Encyclopedia of Mathematics
The function
 | (*) |
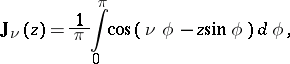which satisfies the inhomogeneous Bessel equation:
 |
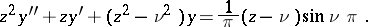For integers 
is the Bessel function of order 
(cf. Bessel functions). For non-integer 
the following expansion is valid:
 |
 |
 |
 |
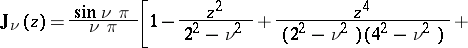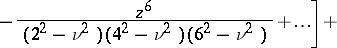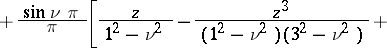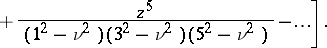The asymptotic expansion
 |
 |
 |
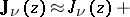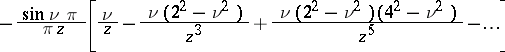is valid for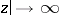 
and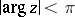 
.
The functions have been named after C.T. Anger [1], who studied functions of the type (*), but with 
as the upper limit of the integral.
References
| [1] | C.T. Anger, Neueste Schr. d. Naturf. d. Ges. i. Danzig , 5 (1855) pp. 1–29 |
| [2] | G.N. Watson, "A treatise on the theory of Bessel functions" , 1–2 , Cambridge Univ. Press (1952) |
How to Cite This Entry:
Anger function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Anger_function&oldid=16115
Anger function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Anger_function&oldid=16115
This article was adapted from an original article by A.P. Prudnikov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article