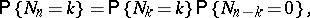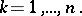A result in the theory of fluctuations in random walks (cf. Random walk). Let 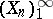 be independent random variables with the same distribution (cf. Random variable), and let
be independent random variables with the same distribution (cf. Random variable), and let  ,
, 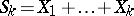 ,
, 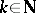 . Define
. Define
Then (equivalence principle) for each 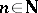 the pairs
the pairs 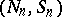 ,
, 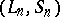 and
and 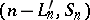 have the same distribution; in particular,
have the same distribution; in particular, 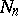 ,
, 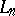 and
and 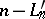 have the same distribution. As a consequence one has
have the same distribution. As a consequence one has
These results were first proved by E. Sparre Andersen [a1], [a2], [a3]. They connect the arcsine law for random walks to the arcsine law in renewal theory.
Nowadays there are brief proofs based on combinatorial properties of non-random sequences [a6], [a7]. The results can be generalized to random vectors with symmetric distributions [a2]. A comprehensive account for integer-valued random variables can be found in [a8]; a concise overview is given in [a4]. Related combinatorial results are discussed in [a5].
References
| [a1] | E. Sparre Andersen, "On the number of positive sums of random variables" Skand. Aktuarietikskr. , 32 (1949) pp. 27–36 |
| [a2] | E. Sparre Andersen, "On sums of symmetrically dependent random variables" Skand. Aktuarietikskr. , 36 (1953) pp. 123–138 |
| [a3] | E. Sparre Andersen, "On the fluctuations of sums of random variables" Math. Scand. , 1 (1953) pp. 263–285 (Also: 2 (1954), 195–223) |
| [a4] | N.H. Bingham, C.M. Goldie, J.L. Teugels, "Regular variation" , Encycl. Math. Appl. , 27 , Cambridge Univ. Press (1989) (Edition: Second) |
| [a5] | N.G. de Bruijn, "Some algorithms for ordering a sequence of objects, with application to E. Sparre Andersen's principle of equivalence in mathematical statistics" Indagationes Mathematicae , 34 : 1 (1972) pp. 1–10 |
| [a6] | W. Feller, "An introduction to probability theory and its applications" , 2 , Springer (1976) (Edition: Second) |
| [a7] | A.W. Joseph, "An elementary proof of the principle of equivalence" J. London Math. Soc. (2) , 3 (1971) pp. 101–102 |
| [a8] | F. Spitzer, "Principles of random walk" , Springer (1976) (Edition: Second) |
How to Cite This Entry:
Andersen theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Andersen_theorem&oldid=14103
This article was adapted from an original article by F.W. Steutel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article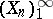 be independent random variables with the same distribution (cf. Random variable), and let
be independent random variables with the same distribution (cf. Random variable), and let  ,
, 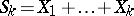 ,
, 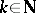 . Define
. Define
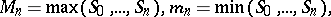
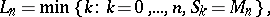
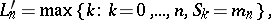
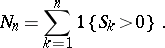
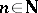 the pairs
the pairs 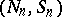 ,
, 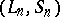 and
and 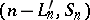 have the same distribution; in particular,
have the same distribution; in particular, 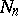 ,
, 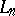 and
and 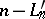 have the same distribution. As a consequence one has
have the same distribution. As a consequence one has