Analytic operator

at a point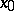

An operator 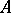, acting from one Banach space into another, that admits a representation of the form

where 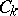is a form of degree 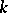and the series converges uniformly in some ball 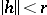. An operator is called analytic in a domain 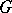if it is an analytic operator at all points of this domain. An analytic operator is infinitely differentiable. In the case of complex spaces, analyticity of an operator in a domain is a consequence of its differentiability (according to Gâteaux) at each point of this domain. Examples of analytic operators are Lyapunov's integro-power series, and the Hammerstein and Urysohn operators with smooth kernels on the space 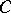of continuous functions.

References

[1]	E. Hille, R.S. Phillips, "Functional analysis and semi-groups" , Amer. Math. Soc. (1957)
[2]	M.A. Krasnosel'skii, G.M. Vainikko, P.P. Zabreiko, et al., "Approximate solution of operator equations" , Wolters-Noordhoff (1972) (Translated from Russian)