Analytic image
An extension of the concept of a complete analytic function, obtained on considering all possible elements of an analytic function in the form of generalized power series (Puiseux series)
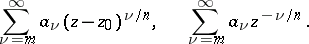 | (*) |
Here  is a complex variable,
is a complex variable,  is an integer and
is an integer and  is a natural number. The series converge in the domains
is a natural number. The series converge in the domains 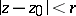 and
and 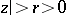 , respectively. An analytic image can be identified with the class of all elements of the form (*) which are obtained from each other by analytic continuation. The analytic image differs from the complete analytic function by the addition of all ramified elements of the form (*) with
, respectively. An analytic image can be identified with the class of all elements of the form (*) which are obtained from each other by analytic continuation. The analytic image differs from the complete analytic function by the addition of all ramified elements of the form (*) with 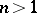 , which are obtained by analytic continuation of its regular elements with
, which are obtained by analytic continuation of its regular elements with  . After the introduction of a suitable topology, the analytic image is converted to the Riemann surface of the given function.
. After the introduction of a suitable topology, the analytic image is converted to the Riemann surface of the given function.
References
| [1] | A.I. Markushevich, "Theory of functions of a complex variable" , 3 , Chelsea (1977) pp. Chapt. 8 (Translated from Russian) |
Analytic image. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Analytic_image&oldid=18574