Analytic function, element of an

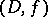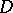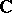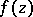The collection of domains in the plane of a complex variable and analytic functions given on 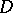by a certain analytic apparatus that allows one to effectively realize the analytic continuation of 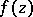to its whole domain of existence as a complete analytic function. The simplest and most frequently used form of an element of an analytic function is the circular element in the form of a power series

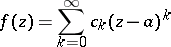(1)

and its disc of convergence 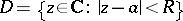with centre at (the centre of the element) and radius of convergence 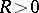. The analytic continuation here is achieved by a (possibly repeated) re-expansion of the series (1) for various centres 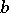, , 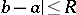by formulas like

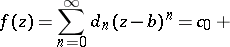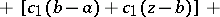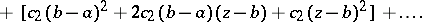Any one of the elements 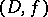of a complete analytic function determines it uniquely and can be represented by means of circular elements with centres 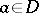. In the case of the centre at infinity, 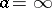, the circular element takes the form

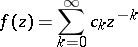with domain of convergence .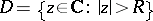

In the process of the analytic continuation, 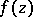may turn out to be multiple-valued and there may appear corresponding algebraic branch points (cf. Algebraic branch point), that is, branched elements of the form

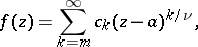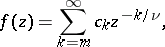where 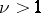; the number 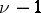is called the branching order. The branched elements generalize the concept of an element of an analytic function, which in this connection is also called an unramified (for 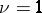) regular (for 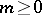) element.

As the simplest element 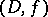of an analytic function 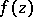of several complex variables 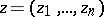, , 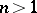one can take a multiple power series

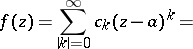(2)

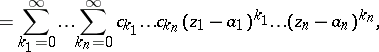where 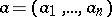is the centre, 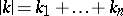, , 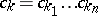, 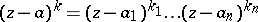and 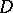is some polydisc

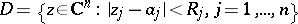in which the series (2) converges absolutely. However, for 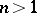one has to bear in mind that a polydisc is not the exact domain of absolute convergence of a power series.

The concept of an element of an analytic function is close to that of the germ of an analytic function.

References

[1]	A.I. Markushevich, "Theory of functions of a complex variable" , 1–2 , Chelsea (1977) (Translated from Russian)
[2]	V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian)

Comments

For 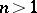the domain of absolute convergence of a power series is a so-called Reinhardt domain, cf. [a1].

References

[a1]	L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) pp. Chapt. 2.4