Difference between revisions of "Analytic function"
m (some TeX) |
m (some Tex) |
||
| Line 31: | Line 31: | ||
\end{equation} | \end{equation} | ||
where | where | ||
| + | \begin{equation} | ||
| + | \frac{\partial f}{\partial x} = \frac{\partial \phi}{\partial x} + i\frac{\partial \psi}{\partial x},\quad \frac{\partial f}{\partial y} = \frac{\partial \phi}{\partial y} + i\frac{\partial \psi}{\partial y}, | ||
| + | \end{equation} | ||
| − | + | are the partial derivatives of $f$. Passing from the independent variables $x, y$ to the variables $z, \overline{z}$, which may formally be considered as new independent variables, related to the old ones by the equations $z = x+iy$, $\overline{z}=x-iy$ (from this point of view, the function $f$ may also be written as $f(z,\overline{z})$) and expressing $dx$ and $dy$ in terms of $dz$ and d\overline{z} according to the usual rules of differential calculus, one can write $df$ in its complex form: | |
| − | + | \begin{equation} | |
| − | are the partial derivatives of | + | df = \frac{\partial f}{\partial z}dz + \frac{\partial f}{\partial \overline{z}}z\overline{z} |
| − | + | \end{equation} | |
| − | |||
where | where | ||
| + | \begin{equation} | ||
| + | \frac{\partial f}{\partial z} = \frac{1}{2}\left(\frac{\partial f}{\partial x} - i\frac{\partial f}{\partial y}\right), \quad \frac{\partial f}{\partial \overline{z}} = \frac{1}{2}\left(\frac{\partial f}{\partial x} + i\frac{\partial f}{\partial y}\right), | ||
| + | \end{equation} | ||
| − | + | are the (formal) derivatives of $f$ with respect to $z$ and $\overline{z}$, respectively. It is seen, accordingly, that $f$ is differentiable in the sense of $\mathbb C$ if and only if it is differentiable in the sense of $\mathbb R^2$ and if the equation $\partial f /\partial\overline{z}=0$ is satisfied, which in expanded form may be written as | |
| − | |||
| − | are the (formal) derivatives of | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012240/a01224067.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012240/a01224067.png" /></td> </tr></table> | ||
Revision as of 08:06, 4 February 2013
A function that can be locally represented by power series. The exceptional importance of the class of analytic functions is due to the following reasons. First, the class is sufficiently large; it includes the majority of functions which are encountered in the principal problems of mathematics and its applications to science and technology. Secondly, the class of analytic functions is closed with respect to the fundamental operations of arithmetic, algebra and analysis. Finally, an important property of an analytic function is its uniqueness: Each analytic function is an "organically connected whole" , which represents a "unique" function throughout its natural domain of existence. This property, which in the 18th century was considered as inseparable from the very notion of a function, became of fundamental significance after a function had come to be regarded, in the first half of the 19th century, as an arbitrary correspondence. The theory of analytic functions originated in the 19th century, mainly due to the work of A.L. Cauchy, B. Riemann and K. Weierstrass. The "transition to the complex domain" had a decisive effect on this theory. The theory of analytic functions was constructed as the theory of functions of a complex variable; at present (the 1970's) the theory of analytic functions forms the main subject of the general theory of functions of a complex variable.
There are different approaches to the concept of analyticity. One definition, which was originally proposed by Cauchy, and was considerably advanced by Riemann, is based on a structural property of the function — the existence of a derivative with respect to the complex variable, i.e. its complex differentiability. This approach is closely connected with geometric ideas. Another approach, which was systematically developed by Weierstrass, is based on the possibility of representing functions by power series; it is thus connected with the analytic apparatus by means of which a function can be expressed. A basic fact of the theory of analytic functions is the identity of the corresponding classes of functions in an arbitrary domain of the complex plane.
Exact definitions are given below. Let $D$ be a domain in the complex plane $\mathbb C$. If to each point $z\in D$ there has been assigned some complex number $w$, then one says that on $D$ a (single-valued) function $f$ of the complex variable $z$ has been defined and one writes: $w=f(z), z\in D$ (or $f:D\to\mathbb C$). The function $w=f(z)=f(x+iy)$ may be regarded as a complex function of two real variables $x$ and $y$, defined in the domain $D\subset\mathbb R^2$ (where $\mathbb R^2$ is the Euclidean plane). To define such a function is tantamount to defining two real functions \begin{equation*} u=\phi(x,y),\quad v=\psi(x,y),\quad (x,y)\in D\quad (w = u+iv). \end{equation*}
Having fixed a point $z\in D$, one gives $z$ the increment $\Delta z = \Delta x+ i\Delta y$ (such that $z+\Delta z \in D$) and considers the corresponding increment of the function $f$: \begin{equation} \Delta f(z) = f(z+\Delta z) - f(z). \end{equation} If \begin{equation} \Delta f(z) = A\Delta z + o(\Delta z) \end{equation} as $\Delta z\to 0$, or in other words, if \begin{equation} \lim_{\Delta z\to 0}\frac{\Delta f(z)}{\Delta z} = A \end{equation} exists, the function $f$ is said to be differentiable (in the sense of complex analysis or in the sense of $\mathbb C$) at $z$; $A = f'(z)$ is the derivative of $f$ at $z$, and \begin{equation} A\Delta z = f'(z)dz = df(z) \end{equation} is its differential at that point. A function $f$ which is differentiable at every point of $D$ is called differentiable in the domain $D$.
One may compare the concepts of differentiability of $f$ considered as a function of two variables (in the sense of $\mathbb R^n$) and in the sense of $\mathbb C$. In the former case the differential $df$ has the form \begin{equation} \frac{\partial f}{\partial x}dx + \frac{\partial f}{\partial y}dy, \end{equation} where \begin{equation} \frac{\partial f}{\partial x} = \frac{\partial \phi}{\partial x} + i\frac{\partial \psi}{\partial x},\quad \frac{\partial f}{\partial y} = \frac{\partial \phi}{\partial y} + i\frac{\partial \psi}{\partial y}, \end{equation}
are the partial derivatives of $f$. Passing from the independent variables $x, y$ to the variables $z, \overline{z}$, which may formally be considered as new independent variables, related to the old ones by the equations $z = x+iy$, $\overline{z}=x-iy$ (from this point of view, the function $f$ may also be written as $f(z,\overline{z})$) and expressing $dx$ and $dy$ in terms of $dz$ and d\overline{z} according to the usual rules of differential calculus, one can write $df$ in its complex form: \begin{equation} df = \frac{\partial f}{\partial z}dz + \frac{\partial f}{\partial \overline{z}}z\overline{z} \end{equation}
where \begin{equation} \frac{\partial f}{\partial z} = \frac{1}{2}\left(\frac{\partial f}{\partial x} - i\frac{\partial f}{\partial y}\right), \quad \frac{\partial f}{\partial \overline{z}} = \frac{1}{2}\left(\frac{\partial f}{\partial x} + i\frac{\partial f}{\partial y}\right), \end{equation}
are the (formal) derivatives of $f$ with respect to $z$ and $\overline{z}$, respectively. It is seen, accordingly, that $f$ is differentiable in the sense of $\mathbb C$ if and only if it is differentiable in the sense of $\mathbb R^2$ and if the equation $\partial f /\partial\overline{z}=0$ is satisfied, which in expanded form may be written as
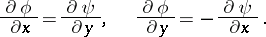 |
If 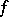 is differentiable in the sense of
is differentiable in the sense of  in
in 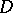 , the latter relations are satisfied at all point of the domain; they are called the Cauchy–Riemann equations. These equations occurred already in the 18th century in J.L. d'Alembert's and L. Euler's studies on functions of a complex variable. The initial definition may now be rendered more precise as follows. A function
, the latter relations are satisfied at all point of the domain; they are called the Cauchy–Riemann equations. These equations occurred already in the 18th century in J.L. d'Alembert's and L. Euler's studies on functions of a complex variable. The initial definition may now be rendered more precise as follows. A function 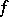 , defined in a domain
, defined in a domain 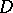 , is said to be holomorphic (analytic) at a point
, is said to be holomorphic (analytic) at a point 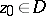 if there exists a neighbourhood of this point in which
if there exists a neighbourhood of this point in which  may be represented by a power series:
may be represented by a power series:
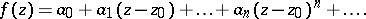 |
If this requirement is satisfied at every point 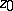 of
of  , the function
, the function 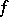 is said to be holomorphic (analytic) in the domain
is said to be holomorphic (analytic) in the domain 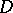 .
.
A function  which is holomorphic at a point
which is holomorphic at a point 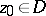 is differentiable at that point. In addition, the sum of a convergent power series has derivatives of all orders (is infinitely differentiable) with respect to the complex variable
is differentiable at that point. In addition, the sum of a convergent power series has derivatives of all orders (is infinitely differentiable) with respect to the complex variable  ; the coefficients of the series may be expressed in terms of the derivatives of
; the coefficients of the series may be expressed in terms of the derivatives of 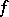 at
at 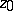 by the formulas
by the formulas 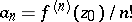 . The power series, written in the form
. The power series, written in the form
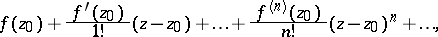 |
is known as the Taylor series of  at
at 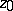 . Thus, holomorphy of a function
. Thus, holomorphy of a function 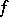 in a domain
in a domain  means that it is infinitely differentiable at any point in
means that it is infinitely differentiable at any point in  and that its Taylor series converges to it in some neighbourhood of this point.
and that its Taylor series converges to it in some neighbourhood of this point.
On the other hand, the following noteworthy fact is established in the theory of analytic functions: If a function 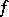 is differentiable in a domain
is differentiable in a domain 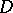 , it is holomorphic in this domain (for a single point this statement is not true:
, it is holomorphic in this domain (for a single point this statement is not true: 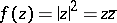 is differentiable at
is differentiable at  , but is nowhere holomorphic). Thus, the concepts of complex differentiability and holomorphy of a function in a domain are identical; each one of the following properties of a function
, but is nowhere holomorphic). Thus, the concepts of complex differentiability and holomorphy of a function in a domain are identical; each one of the following properties of a function 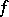 in a domain
in a domain 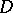 — differentiability in the sense of
— differentiability in the sense of 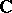 , differentiability in the sense of
, differentiability in the sense of 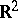 together with satisfaction of the Cauchy–Riemann equations, holomorphy — may serve as definition of analyticity of
together with satisfaction of the Cauchy–Riemann equations, holomorphy — may serve as definition of analyticity of 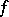 in this domain.
in this domain.
One other characteristic of an analytic function is connected with the notion of an integral. The integral of a function 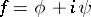 along an (oriented rectifiable) curve
along an (oriented rectifiable) curve 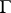 :
: 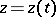 ,
, 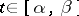 , may be defined by the formula:
, may be defined by the formula:
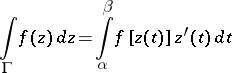 |
or by means of a curvilinear integral:
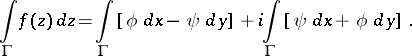 |
A key result in the theory of analytic functions is Cauchy's integral theorem: If 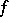 is an analytic function in a domain
is an analytic function in a domain 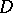 , then
, then 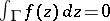 for any closed curve
for any closed curve 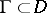 bounding a domain inside
bounding a domain inside 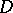 . The converse result (Morera's theorem) is also true: If
. The converse result (Morera's theorem) is also true: If 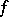 is continuous in a domain
is continuous in a domain 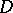 and if
and if 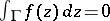 for any such curve
for any such curve  , then
, then 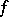 is an analytic function in
is an analytic function in 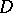 . In particular, in a simply-connected domain, those and only those continuous functions
. In particular, in a simply-connected domain, those and only those continuous functions 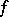 are analytic, whose integral along any closed curve
are analytic, whose integral along any closed curve 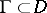 is zero (or, which is the same thing, the integral along any curve
is zero (or, which is the same thing, the integral along any curve 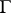 connecting two arbitrary points
connecting two arbitrary points 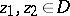 does depend only on the points
does depend only on the points  and
and 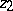 themselves and not on the shape of the curve). This characterization of analytic functions forms the basis of many of their applications.
themselves and not on the shape of the curve). This characterization of analytic functions forms the basis of many of their applications.
Cauchy's integral theorem yields Cauchy's integral formula, which expresses the values of an analytic function inside a domain in terms of its values on the boundary:
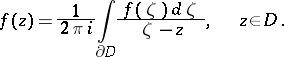 |
Here, 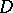 is a domain whose boundary
is a domain whose boundary 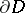 consists of a finite number of non-intersecting rectifiable curves (the orientation of
consists of a finite number of non-intersecting rectifiable curves (the orientation of  is assumed to be positive with respect to
is assumed to be positive with respect to 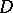 ), and
), and 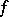 is a function which is analytic in some domain
is a function which is analytic in some domain 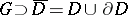 . This formula makes it possible, in particular, to reduce the study of many problems connected with analytic functions to the corresponding problems for a very simple function — the Cauchy kernel
. This formula makes it possible, in particular, to reduce the study of many problems connected with analytic functions to the corresponding problems for a very simple function — the Cauchy kernel 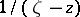 ,
,  ,
, 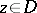 . For more details see Integral representation of an analytic function.
. For more details see Integral representation of an analytic function.
A very important property of analytic functions is expressed by the following uniqueness theorem: Two functions which are analytic in a domain  and which coincide on some set with a limit point in
and which coincide on some set with a limit point in 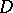 , coincide throughout
, coincide throughout  (are identical). In particular, an analytic function
(are identical). In particular, an analytic function 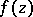 ,
,  , which is not identically zero can only have isolated zeros in
, which is not identically zero can only have isolated zeros in 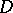 . If, in addition,
. If, in addition, 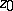 is a zero of
is a zero of 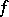 , then one has, in some neighbourhood
, then one has, in some neighbourhood 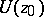 of
of 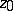 ,
, 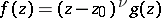 , where
, where 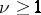 is a natural number (called the multiplicity of the zero of
is a natural number (called the multiplicity of the zero of 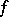 at
at  ), while
), while 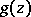 is a analytic function in
is a analytic function in 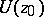 .
.
An important role in the theory of analytic functions is played by the points at which the function is not analytic — the so-called singular points of the analytic function. Here, only isolated singular points of (single-valued) analytic functions are considered; for more details cf. Singular point. If  is an analytic function in an annulus of the form
is an analytic function in an annulus of the form 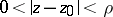 , it may be expanded there in a Laurent series
, it may be expanded there in a Laurent series
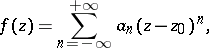 |
which contains, as a rule, not only positive but also negative powers of 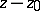 . If there are no terms with negative powers in the series (
. If there are no terms with negative powers in the series (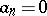 for
for 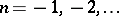 ),
), 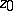 is called a regular point of
is called a regular point of 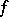 (a removable singular point). At a regular point there also exists a finite limit
(a removable singular point). At a regular point there also exists a finite limit
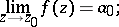 |
Putting  , one obtains an analytic function in the whole disc
, one obtains an analytic function in the whole disc  . If the Laurent series of the function contains only a finite number of terms with negative powers of
. If the Laurent series of the function contains only a finite number of terms with negative powers of 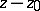 :
:
 |
the point 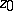 is called a pole of
is called a pole of 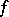 (of multiplicity
(of multiplicity 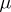 ); a pole
); a pole 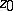 is characterized by
is characterized by
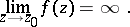 |
The function 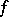 has a pole of multiplicity
has a pole of multiplicity 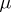 at the point
at the point 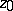 if and only if the function
if and only if the function 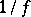 has a zero of multiplicity
has a zero of multiplicity 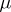 at this point. If the Laurent series contains an infinite number of negative powers of
at this point. If the Laurent series contains an infinite number of negative powers of 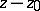 (
( for an infinite set of negative indices
for an infinite set of negative indices  ), then
), then 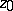 is called an essential singular point; at such points there is no finite and no infinite limit for
is called an essential singular point; at such points there is no finite and no infinite limit for 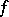 . The coefficient
. The coefficient 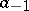 in the Laurent series for
in the Laurent series for  with centre at the isolated singular point
with centre at the isolated singular point 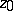 is called the residue of
is called the residue of  at
at 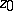 :
:
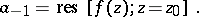 |
It can be defined by the formula
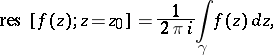 |
where 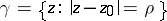 and
and 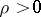 is sufficiently small (so that the disc
is sufficiently small (so that the disc 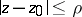 does not contain singular points of
does not contain singular points of 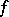 other than
other than 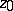 ). The important role of residues is made clear by the following theorem: If
). The important role of residues is made clear by the following theorem: If 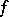 is an analytic function in a domain
is an analytic function in a domain 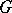 , except for some set of isolated singular points, if
, except for some set of isolated singular points, if 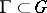 is a contour bounding a domain
is a contour bounding a domain 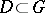 and not passing through any singular points of
and not passing through any singular points of 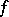 , and if
, and if  are all the singular points of
are all the singular points of 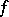 inside
inside 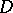 , then
, then
 |
This theorem is an effective tool in calculating integrals. See also Residue of an analytic function.
The sum of the terms of the Laurent series for 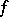 at
at 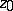 corresponding to the negative indices
corresponding to the negative indices  ,
,
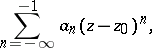 |
is known as the principal part of the Laurent series (or of the function 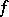 ) at the point
) at the point 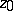 . This principal part determines the nature of the singularity of
. This principal part determines the nature of the singularity of 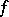 at
at 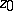 .
.
Functions which are representable as a quotient of two functions that are holomorphic in a domain 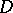 are called meromorphic in the domain
are called meromorphic in the domain 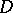 . A function which is meromorphic in a domain is holomorphic in that domain, except possibly at a finite or countable set of poles; at the poles the values of a meromorphic function are considered to be infinite. If such values are allowed, then meromorphic functions in a domain
. A function which is meromorphic in a domain is holomorphic in that domain, except possibly at a finite or countable set of poles; at the poles the values of a meromorphic function are considered to be infinite. If such values are allowed, then meromorphic functions in a domain 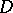 may be defined as functions that in a neighbourhood of each point
may be defined as functions that in a neighbourhood of each point 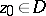 can be represented by a Laurent series in
can be represented by a Laurent series in 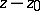 with a finite number of terms involving negative powers of
with a finite number of terms involving negative powers of 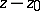 (depending on
(depending on  ) in a neighbourhood of each point
) in a neighbourhood of each point 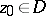 .
.
Both holomorphic and meromorphic functions in a domain 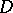 are often designated as analytic in the domain
are often designated as analytic in the domain 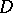 . In this a case holomorphic functions are also said to be regular analytic or simply regular functions.
. In this a case holomorphic functions are also said to be regular analytic or simply regular functions.
The simplest class of analytic functions consists of the functions which are holomorphic in the whole plane; such functions are called entire functions. Entire functions are represented by series  which are convergent in the whole plane. This class includes the polynomials in
which are convergent in the whole plane. This class includes the polynomials in  , the functions
, the functions
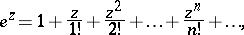 |
 |
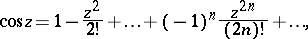 |
etc.
Weierstrass' theorem states that, for any sequence of complex numbers 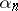 ,
, 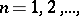 without limit points in
without limit points in 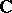 , there exists an entire function
, there exists an entire function 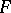 that vanishes at the points
that vanishes at the points 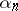 and only at these points (among the
and only at these points (among the 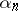 there may be coincident points, to which correspond zeros of
there may be coincident points, to which correspond zeros of 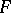 of corresponding multiplicity). Here, the function
of corresponding multiplicity). Here, the function 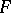 may be represented as a (generally infinite) product of entire functions each one of which has only one zero.
may be represented as a (generally infinite) product of entire functions each one of which has only one zero.
Functions that are meromorphic in the plane (i.e. that may be represented as quotients of entire functions) are called meromorphic functions. These include rational functions, 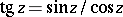 ,
, 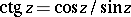 , elliptic functions, etc.
, elliptic functions, etc.
According to Mittag-Leffler's theorem, for any sequence 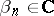 ,
, 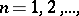 without limit points in
without limit points in 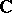 , there exists a meromorphic function
, there exists a meromorphic function 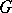 with poles at the points
with poles at the points 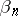 and only at those points, such that its principal parts at the points
and only at those points, such that its principal parts at the points 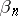 coincide with pre-assigned polynomials in
coincide with pre-assigned polynomials in 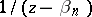 . The function
. The function 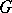 may be represented as a (usually infinite) sum of meromorphic functions, each one with a pole at a single point only.
may be represented as a (usually infinite) sum of meromorphic functions, each one with a pole at a single point only.
Theorems on the existence of a holomorphic function with pre-assigned zeros and of meromorphic functions with pre-assigned poles and principal parts are also valid for an arbitrary domain 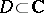 .
.
In the study of analytic functions the related geometric notions are also of importance. If 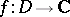 is an analytic function, the image
is an analytic function, the image 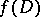 of the domain
of the domain 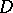 is also a domain (principle of preservation of domains).
is also a domain (principle of preservation of domains). 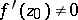 , If the mapping
, If the mapping 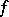 preserves angles at
preserves angles at 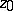 both in value and in sign, i.e. it is conformal. Thus, there exists a close connection between analyticity and the important geometric notion of conformal mapping. If
both in value and in sign, i.e. it is conformal. Thus, there exists a close connection between analyticity and the important geometric notion of conformal mapping. If 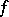 is an analytic function in
is an analytic function in 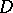 and
and 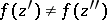 for
for 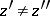 (such functions are called univalent), then
(such functions are called univalent), then 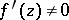 in
in 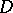 and
and 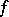 defines a one-to-one and conformal mapping of the domain
defines a one-to-one and conformal mapping of the domain 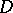 onto the domain
onto the domain 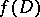 . Riemann's theorem, which is the fundamental theorem in the theory of conformal mappings, says that on any simply-connected domain whose boundary contains more than one point there exist univalent analytic functions which conformally map this domain onto a disc or a half-plane (cf. Conformal mapping; Univalent function).
. Riemann's theorem, which is the fundamental theorem in the theory of conformal mappings, says that on any simply-connected domain whose boundary contains more than one point there exist univalent analytic functions which conformally map this domain onto a disc or a half-plane (cf. Conformal mapping; Univalent function).
The real and imaginary parts of a function 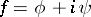 which is holomorphic in a domain
which is holomorphic in a domain 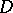 satisfy the Laplace equation in that domain:
satisfy the Laplace equation in that domain:
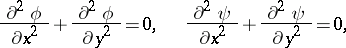 |
i.e. they are harmonic functions (cf. Harmonic function). Two harmonic functions which are connected by the Cauchy–Riemann equations are called conjugate. In a simply-connected domain any harmonic function 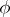 has a conjugate function
has a conjugate function 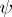 and is thus the real part of some holomorphic function
and is thus the real part of some holomorphic function 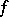 in
in 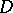 .
.
The connections with conformal mappings and harmonic functions form the basis of many applications of the theory of analytic functions.
A function 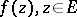 (
(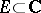 being an arbitrary set), is called analytic at a point
being an arbitrary set), is called analytic at a point 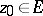 if there exists a neighbourhood of this point such that
if there exists a neighbourhood of this point such that 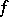 may be represented by a convergent power series on the intersection of this neighbourhood with
may be represented by a convergent power series on the intersection of this neighbourhood with 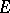 . The function
. The function  is called analytic on the set
is called analytic on the set 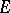 if it is analytic on some open set which contains
if it is analytic on some open set which contains 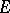 (or, more exactly, if there exist both an open set containing
(or, more exactly, if there exist both an open set containing 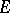 and an analytic function
and an analytic function 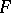 on this set which coincides with
on this set which coincides with 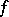 on
on 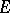 ). For open sets the notion to analyticity coincides with the notion of differentiability with respect to the set. However, this is not the case in general; in particular, on the real line there exist functions which not only have a derivative, but which are infinitely differentiable at every point and are not analytic even at a single point of this line. The property of connectedness of the set
). For open sets the notion to analyticity coincides with the notion of differentiability with respect to the set. However, this is not the case in general; in particular, on the real line there exist functions which not only have a derivative, but which are infinitely differentiable at every point and are not analytic even at a single point of this line. The property of connectedness of the set  is necessary in order that the uniqueness theorem for analytic functions holds. This is why analytic functions are usually considered in domains, i.e. on connected open sets.
is necessary in order that the uniqueness theorem for analytic functions holds. This is why analytic functions are usually considered in domains, i.e. on connected open sets.
All the preceding refers to single-valued analytic functions 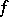 , considered in a given domain
, considered in a given domain 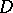 (or on a given set
(or on a given set 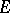 ) of the complex plane. In considering the possible extension of a function
) of the complex plane. In considering the possible extension of a function 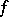 , as an analytic function, to a larger domain, one arrives at the concept of the analytic function considered as a whole, i.e. throughout its whole natural domain of existence. If the function is thus extended, its domain of analyticity becomes larger, and may overlap itself, supplying new values of the function at points in the plane where it already was defined. Accordingly, an analytic function considered as a whole is generally multi-valued. Many problems in analysis (inversion of a function, the determination of a primitive and the construction of an analytic function with a given real part in multiply-connected domains (cf. Multiply-connected domain), the solution of algebraic equations with analytic coefficients, etc.) require the study of multi-valued functions; such functions include
, as an analytic function, to a larger domain, one arrives at the concept of the analytic function considered as a whole, i.e. throughout its whole natural domain of existence. If the function is thus extended, its domain of analyticity becomes larger, and may overlap itself, supplying new values of the function at points in the plane where it already was defined. Accordingly, an analytic function considered as a whole is generally multi-valued. Many problems in analysis (inversion of a function, the determination of a primitive and the construction of an analytic function with a given real part in multiply-connected domains (cf. Multiply-connected domain), the solution of algebraic equations with analytic coefficients, etc.) require the study of multi-valued functions; such functions include 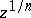 ,
, 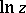 ,
, 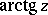 ,
, 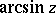 , algebraic functions, etc. (cf. Algebraic function).
, algebraic functions, etc. (cf. Algebraic function).
A regular process which yields the complete analytic function, considered throughout its natural domain of existence, was proposed by Weierstrass; it is known as Weierstrass' method of analytic continuation.
The initial concept is that of an element of an analytic function, viz. a power series with a non-zero radius of convergence. Such an element 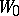 :
:
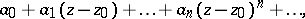 |
defines a certain analytic function 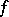 on its disc of convergence
on its disc of convergence 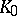 . Let
. Let 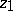 be a point of
be a point of 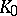 different from
different from 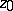 . Expanding
. Expanding 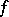 in a series with centre at
in a series with centre at 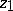 , one obtains a new element
, one obtains a new element 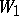 :
:
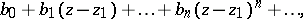 |
whose disc of convergence will be denoted by 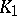 . In the intersection of
. In the intersection of 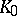 and
and 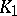 the series
the series 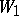 converges to the same function as the series
converges to the same function as the series 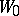 . If
. If 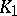 extends beyond the boundary of
extends beyond the boundary of 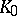 , the series
, the series 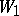 defines the function determined by
defines the function determined by 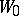 on some set outside
on some set outside 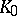 (where the series
(where the series 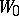 is divergent). In such a case the element
is divergent). In such a case the element 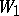 is called a direct analytic continuation of the element
is called a direct analytic continuation of the element 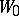 . Let
. Let 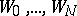 be a chain of elements in which
be a chain of elements in which 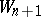 is a direct analytic continuation of
is a direct analytic continuation of 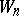 (
(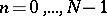 ); the element
); the element 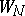 is then said to be an analytic continuation of the element
is then said to be an analytic continuation of the element 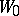 (by means of the given chain of elements). When the centre of the disc
(by means of the given chain of elements). When the centre of the disc  belongs to
belongs to  it may happen that the element
it may happen that the element 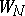 is not a direct analytic continuation of the element
is not a direct analytic continuation of the element 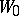 . In such a case the sums of the series
. In such a case the sums of the series  and
and 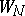 will have different values in the intersection of
will have different values in the intersection of 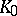 and
and 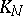 ; thus analytic continuation may lead to new values of the function inside
; thus analytic continuation may lead to new values of the function inside 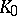 .
.
The totality of all elements which may be obtained by analytic continuation of an element 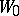 forms the complete analytic function (in the sense of Weierstrass) generated by
forms the complete analytic function (in the sense of Weierstrass) generated by 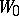 ; the union of their discs of convergence represents the (Weierstrass) domain of existence of this function. It follows from the uniqueness theorem for analytic functions that an analytic function in the sense of Weierstrass is completely determined by the given element
; the union of their discs of convergence represents the (Weierstrass) domain of existence of this function. It follows from the uniqueness theorem for analytic functions that an analytic function in the sense of Weierstrass is completely determined by the given element 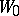 . The initial element may be any other element belonging to this function; the complete analytic function will not be affected.
. The initial element may be any other element belonging to this function; the complete analytic function will not be affected.
A complete analytic function 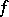 , considered as a function of the points in the plane belonging to its domain of existence
, considered as a function of the points in the plane belonging to its domain of existence 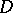 , is generally multi-valued. In order to eliminate this feature,
, is generally multi-valued. In order to eliminate this feature, 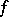 is considered not as a function of the points in the plane domain
is considered not as a function of the points in the plane domain 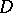 , but rather as a function of the points on some multi-sheeted surface
, but rather as a function of the points on some multi-sheeted surface 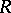 (lying above
(lying above 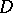 ) such that to each point of
) such that to each point of  there correspond as many points of the surface
there correspond as many points of the surface 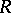 (projecting onto the given point of
(projecting onto the given point of 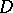 ) as there are different elements with centre at this point in the complete analytic function
) as there are different elements with centre at this point in the complete analytic function 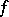 ; on the surface
; on the surface 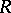 the function
the function  becomes single-valued. The idea of passing to such surfaces is due to Riemann, and the surfaces themselves are known as Riemann surfaces. The abstract definition of the notion of a Riemann surface has made it possible to replace the theory of multi-valued analytic functions by the theory of single-valued analytic functions on Riemann surfaces (cf. Riemann surface).
becomes single-valued. The idea of passing to such surfaces is due to Riemann, and the surfaces themselves are known as Riemann surfaces. The abstract definition of the notion of a Riemann surface has made it possible to replace the theory of multi-valued analytic functions by the theory of single-valued analytic functions on Riemann surfaces (cf. Riemann surface).
Now fix a domain 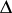 belonging to the domain of existence
belonging to the domain of existence 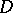 of the complete analytic function
of the complete analytic function 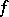 , and fix some element
, and fix some element 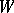 of
of 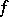 with centre at a point in
with centre at a point in 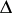 . The totality of all elements which may be obtained by analytic continuation of
. The totality of all elements which may be obtained by analytic continuation of 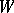 by means of chains with centres belonging to
by means of chains with centres belonging to 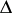 is called a branch of the analytic function
is called a branch of the analytic function 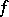 . A branch of a multi-valued analytic function may turn out to be a single-valued analytic function in the domain
. A branch of a multi-valued analytic function may turn out to be a single-valued analytic function in the domain 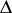 . Thus, arbitrary branches of the functions
. Thus, arbitrary branches of the functions 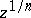 and
and 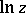 which correspond to an arbitrary simply-connected domain not containing the point 0, are single-valued functions. The function
which correspond to an arbitrary simply-connected domain not containing the point 0, are single-valued functions. The function 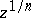 has exactly
has exactly  different branches in such a domain, while
different branches in such a domain, while 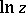 has an infinite set of such branches. The selection of single-valued branches (using some cuts in the domain of existence) and their study by the theory of single-valued analytic functions constitute one of the principal methods of studying specific multi-valued analytic functions.
has an infinite set of such branches. The selection of single-valued branches (using some cuts in the domain of existence) and their study by the theory of single-valued analytic functions constitute one of the principal methods of studying specific multi-valued analytic functions.
A.A. Gonchar
Analytic functions of several complex variables.
The complex space 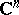 , consisting of the points
, consisting of the points  ,
, 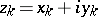 , is a vector space over the field of complex numbers with the Euclidean metric
, is a vector space over the field of complex numbers with the Euclidean metric
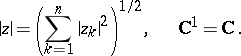 |
It differs from the 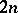 -dimensional Euclidean space
-dimensional Euclidean space 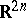 by a certain asymmetry: on passing from
by a certain asymmetry: on passing from 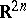 to
to 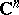 (i.e. on introducing a complex structure in
(i.e. on introducing a complex structure in 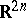 ), the coordinates are subdivided into pairs which appear in the complex combinations
), the coordinates are subdivided into pairs which appear in the complex combinations 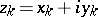 .
.
If a complex function 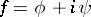 is defined in a domain
is defined in a domain  and is differentiable at all points
and is differentiable at all points 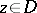 in the sense of
in the sense of 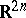 (i.e. as a function of the
(i.e. as a function of the 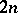 real variables
real variables 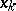 and
and 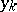 ), its differential may be represented in the form
), its differential may be represented in the form
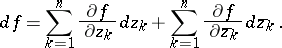 |
Here 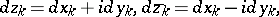 while the symbols
while the symbols 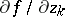 and
and 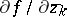 are defined as in the case of the plane. If
are defined as in the case of the plane. If 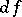 is of the form
is of the form
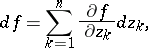 |
i.e. is a complex linear function in 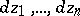 , the function
, the function 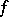 is said to differentiable in the sense of
is said to differentiable in the sense of 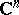 or holomorphic or analytic in the domain
or holomorphic or analytic in the domain 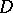 .
.
Thus, the condition of holomorphy of 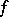 in a domain
in a domain 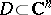 consists of the condition that it be differentiable in the sense of
consists of the condition that it be differentiable in the sense of 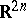 and that it satisfy the system of
and that it satisfy the system of  complex equations
complex equations 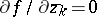 (
(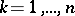 ), which is equivalent to the system of
), which is equivalent to the system of 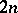 first-order partial differential equations
first-order partial differential equations
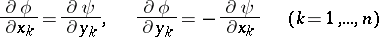 |
(Cauchy–Riemann system).
In the case of space (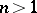 ) as distinct from that of the plane (
) as distinct from that of the plane (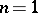 ) this system is overdetermined, since the number of equations is larger than that of the unknown functions. It remains overdetermined on passing to the (geometrically more natural) spatial analogue of a holomorphic function of one complex variable — a holomorphic mapping
) this system is overdetermined, since the number of equations is larger than that of the unknown functions. It remains overdetermined on passing to the (geometrically more natural) spatial analogue of a holomorphic function of one complex variable — a holomorphic mapping 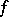 , which is realized by a system
, which is realized by a system 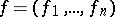 of
of  functions
functions 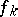 which are holomorphic in a domain
which are holomorphic in a domain  . The mapping
. The mapping 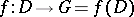 is called biholomorphic if it is one-to-one and if it is holomorphic together with its inverse
is called biholomorphic if it is one-to-one and if it is holomorphic together with its inverse 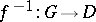 . The conditions for holomorphy of a mapping
. The conditions for holomorphy of a mapping 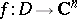 are expressed by a system of
are expressed by a system of 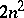 real equations involving
real equations involving 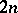 real functions. The overdeterminacy of the conditions of holomorphy for
real functions. The overdeterminacy of the conditions of holomorphy for 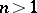 is the cause of a number of effects typical of the spatial case — such as the absence of a spatial analogue of the Riemann theorem on the existence of conformal mappings. According to Riemann's theorem, if
is the cause of a number of effects typical of the spatial case — such as the absence of a spatial analogue of the Riemann theorem on the existence of conformal mappings. According to Riemann's theorem, if 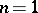 , any two simply-connected domains whose boundaries do not reduce to a single point are isomorphic. However, if
, any two simply-connected domains whose boundaries do not reduce to a single point are isomorphic. However, if 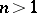 , even such simple simply-connected domains as the ball
, even such simple simply-connected domains as the ball 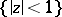 and the product of discs (polydisc)
and the product of discs (polydisc) 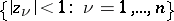 are non-isomorphic. The non-isomorphism is brought to light on comparing the groups of automorphisms of these domains (i.e. their biholomorphic mappings onto themselves, cf. Biholomorphic mapping) — the groups prove to be algebraically non-isomorphic, whereas a biholomorphic mapping of one domain onto another, if it existed, would establish an isomorphism of these groups. Owing to this, the theory of biholomorphic mappings of domains in complex space is substantially different from the theory of conformal mappings in the plane.
are non-isomorphic. The non-isomorphism is brought to light on comparing the groups of automorphisms of these domains (i.e. their biholomorphic mappings onto themselves, cf. Biholomorphic mapping) — the groups prove to be algebraically non-isomorphic, whereas a biholomorphic mapping of one domain onto another, if it existed, would establish an isomorphism of these groups. Owing to this, the theory of biholomorphic mappings of domains in complex space is substantially different from the theory of conformal mappings in the plane.
A function 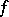 is called holomorphic at a point
is called holomorphic at a point 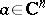 if it is holomorphic in some neighbourhood of this point. According to the Cauchy–Riemann criterion, a function of several variables which is holomorphic at a point
if it is holomorphic in some neighbourhood of this point. According to the Cauchy–Riemann criterion, a function of several variables which is holomorphic at a point  is holomorphic with respect to each variable (if the values of the other variables are fixed). The converse proposition is also true: If, in a neighbourhood of some point, a function
is holomorphic with respect to each variable (if the values of the other variables are fixed). The converse proposition is also true: If, in a neighbourhood of some point, a function 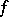 is holomorphic with respect to each variable separately, then it is holomorphic at this point (Hartogs' fundamental theorem).
is holomorphic with respect to each variable separately, then it is holomorphic at this point (Hartogs' fundamental theorem).
In analogy with the case of the plane the holomorphy of a function 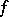 at a point
at a point 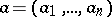 is equivalent to its expandability in a multiple power series in a neighbourhood of this point
is equivalent to its expandability in a multiple power series in a neighbourhood of this point
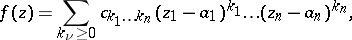 |
or, in abbreviated notation,
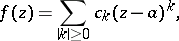 |
where 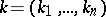 is a multi-index of integers
is a multi-index of integers 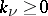 ,
, 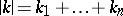 and
and
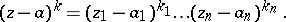 |
A holomorphic function is infinitely differentiable, and the above series is its Taylor series, i.e.
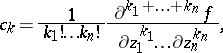 |
the derivatives being taken at the point  .
.
The fundamental facts of the theory of holomorphic functions of one variable extend to holomorphic functions of several variables, sometimes in an altered form. An instance of this is the Weierstrass preparation theorem (cf. Weierstrass theorem), which extends the property of holomorphic functions of one variable to become zero as an integral power of 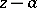 to the spatial case. The theorem is formulated as follows: If a function
to the spatial case. The theorem is formulated as follows: If a function  which is holomorphic at a point
which is holomorphic at a point 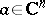 is equal to zero at that point, then it may be represented, in a certain neighbourhood
is equal to zero at that point, then it may be represented, in a certain neighbourhood 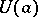 (possibly after a non-degenerate linear transformation of the independent variables) in the form
(possibly after a non-degenerate linear transformation of the independent variables) in the form
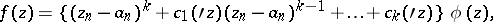 |
where 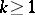 is an integer,
is an integer, 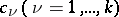 are functions of
are functions of 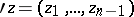 which are holomorphic in a neighbourhood of the point
which are holomorphic in a neighbourhood of the point 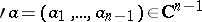 (a "prime" preceding a letter denotes the projection on the space of the first
(a "prime" preceding a letter denotes the projection on the space of the first 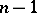 coordinates) and which are equal to zero at
coordinates) and which are equal to zero at  , while
, while 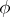 is holomorphic and zero-free in
is holomorphic and zero-free in 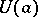 .
.
This theorem is of fundamental importance in the study of analytic sets (cf. Analytic set), which are described locally, in a neighbourhood of each one of their points, as sets of common zeros of a certain number of functions which are holomorphic at this point. By Weierstrass' preparation theorem such sets may be locally described as sets of common zeros of polynomials in the variable 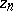 , with coefficients from the ring of holomorphic functions in the other variables
, with coefficients from the ring of holomorphic functions in the other variables 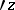 . This circumstance permits extensive use of algebraic methods in the local study of analytic sets.
. This circumstance permits extensive use of algebraic methods in the local study of analytic sets.
Cauchy's integral theorem must also be slightly modified in the spatial case, and is then known as the Cauchy–Poincaré theorem: Let a function 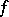 be holomorphic in a domain
be holomorphic in a domain 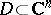 ; then, for any
; then, for any 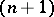 -dimensional surface
-dimensional surface 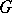 compactly imbedded in
compactly imbedded in 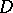 , with piecewise-smooth boundary
, with piecewise-smooth boundary 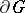 ,
,
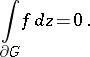 |
As in the planar case, this integral is defined by a parametric representation of the given set: If  has the equation
has the equation 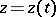 , where the parameter
, where the parameter 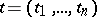 varies over an
varies over an  -dimensional cell
-dimensional cell  , then, by definition,
, then, by definition,
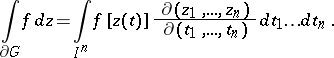 |
The difference between the spatial and the planar cases consists in the fact that in the former case the dimension of the surface 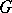 is less than that of the domain
is less than that of the domain 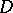 , while in the planar case the dimensions are the same
, while in the planar case the dimensions are the same 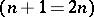 .
.
The spatial analogue of the Cauchy integral formula can be written in a particularly simple form for polycylinder domains, i.e. for products of plane domains. Let 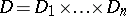 be a domain in which
be a domain in which 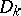 is a domain in the complex plane with a piecewise-smooth boundary
is a domain in the complex plane with a piecewise-smooth boundary 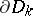 (
(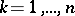 ), while the function
), while the function 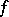 is holomorphic in a domain which compactly contains
is holomorphic in a domain which compactly contains 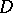 . Successive application of Cauchy's formula for one variable then yields, for any point
. Successive application of Cauchy's formula for one variable then yields, for any point 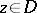 ,
,
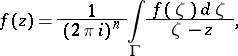 |
where 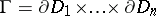 is an
is an  -dimensional surface in the boundary
-dimensional surface in the boundary 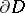 ,
, 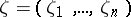 , and
, and
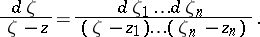 |
However, polycylinder domains are only a very special class, and in general domains such a separation of variables is not possible. The role of Cauchy's integral for arbitrary domains 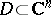 with a piecewise-smooth boundary is played by the Martinelli–Bochner integral formula: For any function
with a piecewise-smooth boundary is played by the Martinelli–Bochner integral formula: For any function 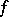 which is holomorphic in a domain containing
which is holomorphic in a domain containing 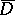 , and for any point
, and for any point 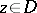 ,
,
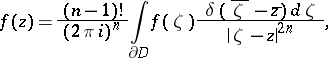 |
where 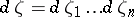 , and
, and
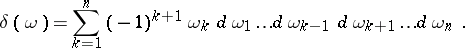 |
This is Green's formula for a pair of functions, one of which is holomorphic in 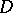 , while the other is a fundamental solution of the Laplace equation in the space
, while the other is a fundamental solution of the Laplace equation in the space 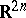 with singular point
with singular point 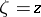 . If
. If 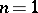 , this is the ordinary Cauchy integral. If
, this is the ordinary Cauchy integral. If  , the formula differs from Cauchy's multiple integral for a product of plane domains in that, first, the integration is not over an
, the formula differs from Cauchy's multiple integral for a product of plane domains in that, first, the integration is not over an  -dimensional part of the boundary, but over the whole
-dimensional part of the boundary, but over the whole 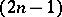 -dimensional boundary of the domain, and, secondly, its kernel (the factor multiplying
-dimensional boundary of the domain, and, secondly, its kernel (the factor multiplying 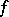 under the integral sign) does not depend analytically on the parameter
under the integral sign) does not depend analytically on the parameter  . An analytic kernel, however, is essential in a number of problems, and it is therefore desirable to construct an integral formula with such a kernel for as large a class of domains as possible. An ample supply of integral formulas, including formulas with an analytic kernel for many domains, is contained in the general Leray formula. This formula is
. An analytic kernel, however, is essential in a number of problems, and it is therefore desirable to construct an integral formula with such a kernel for as large a class of domains as possible. An ample supply of integral formulas, including formulas with an analytic kernel for many domains, is contained in the general Leray formula. This formula is
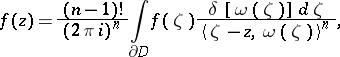 |
where 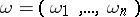 is a smooth vector function depending also on
is a smooth vector function depending also on  ,
, 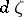 and
and 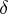 are defined above, and
are defined above, and 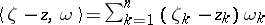 ; it is assumed that
; it is assumed that 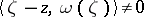 for any fixed
for any fixed 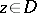 and
and 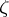 running over
running over  . The value of the integral in this formula does not depend on the choice of the vector function
. The value of the integral in this formula does not depend on the choice of the vector function 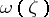 (provided that
(provided that 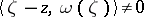 for all
for all 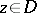 ,
, 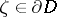 ), and if
), and if 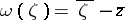 , this integral coincides with the Martinelli–Bochner integral. By varying the choice of
, this integral coincides with the Martinelli–Bochner integral. By varying the choice of 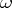 for different classes of domains, the Leray formula will yield various integral formulas. In the theory of analytic functions of several variables other integral representations, which are valid only for certain classes of domains, are also considered. An important class of this kind consists of the so-called Weil domains, which are a generalization of the product of plane domains. For such domains one has the Bergman–Weil representation with a kernel which also depends analytically on the parameter.
for different classes of domains, the Leray formula will yield various integral formulas. In the theory of analytic functions of several variables other integral representations, which are valid only for certain classes of domains, are also considered. An important class of this kind consists of the so-called Weil domains, which are a generalization of the product of plane domains. For such domains one has the Bergman–Weil representation with a kernel which also depends analytically on the parameter.
As in the planar case, the study of the singularities of analytic functions is of fundamental interest; the main difference between the planar and the spatial cases is expressed by the Osgood–Brown theorem on the removability of compact singularities, according to which any function 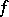 which is holomorphic in
which is holomorphic in 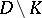 , where
, where 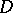 is a domain in
is a domain in 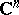 (
(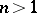 ) and
) and 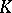 is compact subset of
is compact subset of 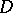 which does not subdivide
which does not subdivide 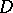 , extends holomorphically to the whole domain
, extends holomorphically to the whole domain  . By this theorem, holomorphic functions of several variables cannot have isolated singular points. These are replaced in
. By this theorem, holomorphic functions of several variables cannot have isolated singular points. These are replaced in 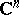 (
(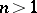 ) by singular sets which are analytic if their dimension is lower than
) by singular sets which are analytic if their dimension is lower than  .
.
This fact is essential in the theory of multi-dimensional residues. This theory deals with the problem of computing the integral of a function 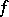 , which is holomorphic everywhere in a domain
, which is holomorphic everywhere in a domain 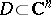 except for an analytic set
except for an analytic set 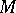 , over a closed
, over a closed  -dimensional surface
-dimensional surface 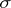 not intersecting
not intersecting 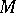 . Since the dimension of the singular set
. Since the dimension of the singular set 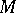 is lower than the dimension of
is lower than the dimension of 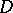 by at least two,
by at least two, 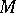 does not subdivide
does not subdivide  . If the surface
. If the surface 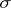 is not linked with
is not linked with 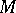 , i.e. bounds an
, i.e. bounds an 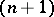 -dimensional surface
-dimensional surface  compactly belonging to
compactly belonging to 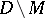 , then by the Cauchy–Poincaré theorem
, then by the Cauchy–Poincaré theorem 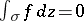 . In order to calculate this integral in the general case, it is necessary to clarify how
. In order to calculate this integral in the general case, it is necessary to clarify how 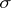 is linked with the singular set
is linked with the singular set 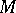 , and to calculate the integrals over special
, and to calculate the integrals over special  -dimensional surfaces associated with separate portions of the set
-dimensional surfaces associated with separate portions of the set 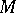 (residues).
(residues).
The solution of this problem involves considerable topological and analytic difficulties. These may often be overcome by the methods proposed by E. Martinelli and J. Leray. The Martinelli method is based on the use of the topological Aleksander–Pontryagin duality principle, and reduces the study of the  -dimensional homologies of the set
-dimensional homologies of the set 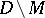 to the study of the
to the study of the 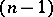 -dimensional homologies of the singular set
-dimensional homologies of the singular set 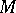 . The Leray method is more general: it is based on the examination of special homology classes and on the calculation of certain differential forms (residue forms). The multi-dimensional theory of residues has also found applications in theoretical physics (cf. Feynman integral).
. The Leray method is more general: it is based on the examination of special homology classes and on the calculation of certain differential forms (residue forms). The multi-dimensional theory of residues has also found applications in theoretical physics (cf. Feynman integral).
The Osgood–Brown theorem reveals an important fundamental difference between the spatial and the planar theories. In the plane one can, for any domain 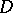 , construct a function
, construct a function 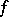 which is holomorphic in
which is holomorphic in 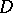 but which cannot be extended analytically beyond its boundary, i.e.
but which cannot be extended analytically beyond its boundary, i.e. 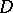 is the natural domain of existence. In space the situation is different: thus, the spherical shell
is the natural domain of existence. In space the situation is different: thus, the spherical shell 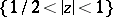 cannot be the domain of existence of any holomorphic function, since by the Osgood–Brown theorem, any function which is holomorphic in it will certainly extend analytically to the entire ball
cannot be the domain of existence of any holomorphic function, since by the Osgood–Brown theorem, any function which is holomorphic in it will certainly extend analytically to the entire ball 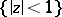 .
.
Thus arises the problem of the characterization of the natural domains of existence of holomorphic functions — the so-called domains of holomorphy. A simple sufficient condition may be formulated with the aid of the concept of a barrier at a boundary point of the domain, i.e. a function 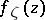 which is holomorphic in this domain and which increases without limit as
which is holomorphic in this domain and which increases without limit as  tends to
tends to 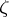 .
. 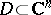 will be a domain of holomorphy if it is possible to construct a barrier for an everywhere-dense set of points in its boundary. This condition is satisfied, in particular, by any convex domain; for any point
will be a domain of holomorphy if it is possible to construct a barrier for an everywhere-dense set of points in its boundary. This condition is satisfied, in particular, by any convex domain; for any point 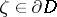 it is sufficient to select, in the
it is sufficient to select, in the 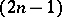 -dimensional supporting plane to
-dimensional supporting plane to 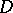 at the point
at the point 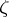 , a
, a  -dimensional plane of the form
-dimensional plane of the form
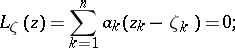 |
the function 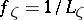 will then be a barrier. Consequently, every convex domain in
will then be a barrier. Consequently, every convex domain in 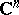 is a domain of holomorphy. However, convexity is not a necessary condition for holomorphy: A product of plane domains is always a domain of holomorphy, and such a product need not be convex. Nevertheless, if the notion of convexity is suitably generalized, it is possible to arrive at a necessary and sufficient condition. One such generalization is based on the observation that the convex hull of a set
is a domain of holomorphy. However, convexity is not a necessary condition for holomorphy: A product of plane domains is always a domain of holomorphy, and such a product need not be convex. Nevertheless, if the notion of convexity is suitably generalized, it is possible to arrive at a necessary and sufficient condition. One such generalization is based on the observation that the convex hull of a set 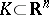 may be described as the set of points at which the value of any linear function does not exceed the supremum of the values of this function on
may be described as the set of points at which the value of any linear function does not exceed the supremum of the values of this function on  . By analogy, the holomorphically convex hull of a set
. By analogy, the holomorphically convex hull of a set 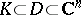 is defined by
is defined by
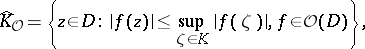 |
where 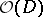 denotes the set of all functions which are holomorphic in
denotes the set of all functions which are holomorphic in 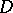 . A domain
. A domain 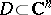 is called holomorphically convex if, for every compact subset
is called holomorphically convex if, for every compact subset 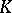 of
of 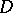 , the hull
, the hull 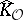 also is a compact subset of
also is a compact subset of 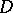 . Holomorphic convexity is a necessary and sufficient condition for a domain of holomorphy. However, this criterion is not very effective, since holomorphic convexity is difficult to verify.
. Holomorphic convexity is a necessary and sufficient condition for a domain of holomorphy. However, this criterion is not very effective, since holomorphic convexity is difficult to verify.
Another generalization is connected with the notion of a plurisubharmonic function, which is the complex analogue of a convex function. A convex function in a domain 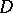 of
of 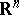 may be defined as a function for which the restrictions to the segments in
may be defined as a function for which the restrictions to the segments in 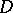 of the straight lines
of the straight lines 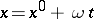 (where
(where 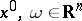 and
and 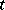 is a real parameter) are convex functions of
is a real parameter) are convex functions of 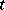 . A real function
. A real function 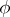 , defined and upper semi-continuous in a domain
, defined and upper semi-continuous in a domain 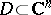 , is said to be plurisubharmonic in
, is said to be plurisubharmonic in 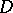 if for each complex line
if for each complex line 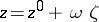 (
(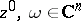 ,
, 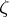 is a complex parameter), its restriction to the parts of this line in
is a complex parameter), its restriction to the parts of this line in 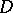 is a subharmonic function of
is a subharmonic function of 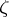 . If
. If 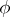 is twice continuously differentiable, then the condition of plurisubharmonicity, in accordance with the rules of differentiation of composite functions, is that the Hermitian form
is twice continuously differentiable, then the condition of plurisubharmonicity, in accordance with the rules of differentiation of composite functions, is that the Hermitian form
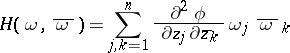 |
— the so-called Levi form — be non-negative.
A domain  is called pseudo-convex if the function
is called pseudo-convex if the function 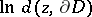 , where
, where 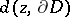 denotes the Euclidean distance from the point
denotes the Euclidean distance from the point 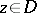 to the boundary
to the boundary 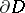 , is plurisubharmonic in this domain. Pseudo-convexity is also a necessary and sufficient condition for a domain to be a domain of holomorphy.
, is plurisubharmonic in this domain. Pseudo-convexity is also a necessary and sufficient condition for a domain to be a domain of holomorphy.
In some cases it is possible to verify effectively the pseudo-convexity of a domain.
As regards domains 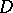 which are not domains of holomorphy, there arises the problem of describing their envelope of holomorphy, i.e. the smallest domain of holomorphy to which any function holomorphic in
which are not domains of holomorphy, there arises the problem of describing their envelope of holomorphy, i.e. the smallest domain of holomorphy to which any function holomorphic in 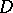 extends analytically. For domains of the simplest types envelopes of holomorphy can be effectively constructed, but in the general case the problem is unsolvable within the class of single-sheeted domains. Under analytic continuation of functions beyond the boundary of a given domain
extends analytically. For domains of the simplest types envelopes of holomorphy can be effectively constructed, but in the general case the problem is unsolvable within the class of single-sheeted domains. Under analytic continuation of functions beyond the boundary of a given domain 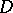 , multi-valuedness may result, which can be avoided by introducing multi-sheeted covering domains over
, multi-valuedness may result, which can be avoided by introducing multi-sheeted covering domains over 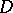 , analogous to Riemann surfaces (cf. Riemann surface). In the class of covering domains, the problem of constructing envelopes of holomorphy is always solvable. This problem also has applications in theoretical physics, to wit in quantum field theory.
, analogous to Riemann surfaces (cf. Riemann surface). In the class of covering domains, the problem of constructing envelopes of holomorphy is always solvable. This problem also has applications in theoretical physics, to wit in quantum field theory.
The transition from the plane to a complex space substantially increases the variety of geometrical problems related to holomorphic functions. In particular, such functions are naturally considered not only in domains, but also on complex manifolds — smooth manifolds of even real dimension, the neighbourhood relations of which are biholomorphic. Among these, Stein manifolds (cf. Stein manifold) — natural generalizations of domains of holomorphy — play a special role
Several problems in analysis may be reduced to the problem of constructing, in a given domain, a holomorphic function with given zeros or a meromorphic function with given poles and principal parts of the Laurent series. In the plane case, these problems have been solved for arbitrary domains by the theorems of Weierstrass and Mittag-Leffler and their generalizations. The spatial case is different — the solvability of the corresponding problems, the so-called Cousin problems, depends on certain topological and analytic properties of the complex manifolds considered.
The key step in the solution of the Cousin problems is to construct — starting from locally-defined functions with given properties — a global function, defined on the whole manifold under consideration and having the same local properties. Such kinds of constructions are very conveniently effected using the theory of sheaves, which arose from the algebraic-topological treatment of the concept of an analytic function, and which has found important applications in various branches of mathematics. The solution of the Cousin problems by methods of the theory of sheaves was realized by H. Cartan and J.-P. Serre.
B.V. Shabat
The contemporary theory of analytic functions and their generalizations.
This is one of the most important branches of analysis, it is closely connected with quite diverse branches of mathematics and it has numerous applications in theoretical physics, mechanics and technology.
Fundamental investigations on the theory of analytic functions have been carried out by Soviet mathematicians. Extensive interest in the theory of functions of a complex variable emerged in the Soviet Union at the beginning of the 20th century. This was in connection with noteworthy investigations by Soviet scientists on applications of the theory of analytic functions to various problems in the mechanics of continuous media. N.E. Zhukovskii and S.A. Chaplygin solved very important problems in hydrodynamics and aerodynamics by using methods of the theory of analytic functions. In the works of G.V. Kolosov and N.I. Muskhelishvili these methods were applied to fundamental problems in the theory of elasticity. In subsequent years the theory of functions of a complex variable underwent extensive development. The development of various aspects of the theory of analytic functions was determined by the fundamental research of, among others, V.V. Golubev, N.N. Luzin, I.I. Privalov and V.I. Smirnov (boundary properties), M.A. Lavrent'ev (geometric theory, quasi-conformal mappings and their applications to gas dynamics), M.V. Keldysh, M.A. Lavrent'ev and L.I. Sedov (applications to problems in the mechanics of continuous media), D.E. Men'shov (theory of monogeneity), M.V. Keldysh, M.A. Lavrent'ev and S.N. Mergelyan (approximation theory), I.N. Vekua (theory of generalized analytic functions and their applications), A.O. Gel'fond (theory of interpolation), N.N. Bogolyubov and V.S. Vladimirov (theory of analytic functions of several variables and its application to quantum field theory). The development of the theory of analytic functions of one and several complex variables and their generalizations is continuing. See Boundary properties of analytic functions; Quasi-conformal mapping; Boundary value problems of analytic function theory; Approximation of functions of a complex variable.
References
| [1] | I.I. [I.I. Privalov] Priwalow, "Einführung in die Funktionentheorie" , 1–3 , Teubner (1958–1959) (Translated from Russian) MR0342680 MR0264037 MR0264036 MR0264038 MR0123686 MR0123685 MR0098843 Zbl 0177.33401 Zbl 0141.26003 Zbl 0141.26002 Zbl 0082.28802 |
| [2] | V.I. Smirnov, "A course of higher mathematics" , III-2 , Addison-Wesley (1964) (Translated from Russian) MR0182690 MR0182688 MR0182687 MR0177069 MR0168707 Zbl 0122.29703 Zbl 0121.25904 Zbl 0118.28402 Zbl 0117.03404 |
| [3] | A.I. Markushevich, "Theory of functions of a complex variable" , 1–3 , Chelsea (1977) (Translated from Russian) MR0444912 Zbl 0357.30002 |
| [4] | M.A. Lavrent'ev, B.V. Shabat, "Methoden der komplexen Funktionentheorie" , Deutsch. Verlag Wissenschaft. (1967) (Translated from Russian) |
| [5] | G.M. Goluzin, "Geometric theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) MR0247039 Zbl 0183.07502 |
| [6] | M.A. Evgrafov, "Analytic functions" , Saunders , Philadelphia (1966) (Translated from Russian) MR0197686 Zbl 0147.32605 |
| [7] | A.G. Sveshnikov, A.N. Tikhonov, "The theory of functions of a complex variables" , Moscow (1967) (In Russian) MR0722295 MR0349962 MR0349961 |
| [8] | B.A. Fuks, "Theory of analytic functions of several complex variables" , 1–2 , Amer. Math. Soc. (1963–1965) (Translated from Russian) MR0188477 MR0174786 MR0168793 MR0155003 MR0037915 MR0027069 Zbl 0146.30802 Zbl 0138.30902 Zbl 0040.19002 |
| [9] | V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian) |
| [10] | A.I. Markushevich, "Notes on the history of the theory of analytic functions" , Moscow-Leningrad (1951) (In Russian) |
| [11] | , Mathematics in the USSR during thirty years: 1917–1947 , Moscow-Leningrad (1948) pp. 319–414 (In Russian) |
| [12] | , Mathematics in the USSR during 40 years: 1917–1957 , 1 , Moscow (1959) pp. 381–510 (In Russian) |
| [13] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian) Zbl 0799.32001 Zbl 0732.32001 Zbl 0732.30001 Zbl 0578.32001 Zbl 0574.30001 |
| [14] | A.V. Bitsadze, "Fundamentals of the theory of analytic functions of a complex variable" , Moscow (1972) (In Russian) |
A.A. GoncharB.V. Shabat
Comments
Complex analysis, the theory of analytic functions, has been an active field of research up to the present time also in the West. Some of the history may be found in the extensive article in the Encyclopaedia Britannica entitled Analysis, complex.
There is a large number of textbooks on complex analysis besides those listed above. Some good current books are listed below: [a1]–[a10] for the case of one variable, [a11]–[a18] for the case of several variables.
Some final comments on complex analysis of several variables are in order. The "Osgood–Brown theorem on the removability of compact singularities" is usually called the Hartogs extension theorem in the West. The modern proof, due to L. Ehrenpreis, makes use of the inhomogeneous Cauchy–Riemann or  -equations. The so-called
-equations. The so-called 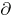 -method, extensively developed by J.J. Kohn and L. Hörmander, has become one of the three most powerful techniques available in complex analysis today. Among other things, it can be used to obtain solutions of the Levi problem (are domains of holomorphy the same as pseudo-convex domains?) and the Cousin problems, cf. [a15]. These fundamental problems had been settled previously by methods now belonging to sheaf theory, and which go back to K. Oka (1936–1954), and have culminated in the sheaf-cohomology theory of H. Cartan, J.-P. Serre, H. Grauert and others, cf. the elegant treatment in [a12]. The third and most recent technique consists in the use of suitable integral representations as developed by G.M. Henkin [G.M. Khenkin] and E. Ramirez de Arellano, cf. [a14].
-method, extensively developed by J.J. Kohn and L. Hörmander, has become one of the three most powerful techniques available in complex analysis today. Among other things, it can be used to obtain solutions of the Levi problem (are domains of holomorphy the same as pseudo-convex domains?) and the Cousin problems, cf. [a15]. These fundamental problems had been settled previously by methods now belonging to sheaf theory, and which go back to K. Oka (1936–1954), and have culminated in the sheaf-cohomology theory of H. Cartan, J.-P. Serre, H. Grauert and others, cf. the elegant treatment in [a12]. The third and most recent technique consists in the use of suitable integral representations as developed by G.M. Henkin [G.M. Khenkin] and E. Ramirez de Arellano, cf. [a14].
References
| [a1] | L.V. Ahlfors, "Complex analysis" , McGraw-Hill (1966) MR0188405 Zbl 0154.31904 |
| [a2] | J.B. Conway, "Functions of one complex variable" , Springer (1973) MR0447532 Zbl 0277.30001 |
| [a3] | A. Dinghas, "Vorlesungen über Funktionentheorie" , Springer (1961) MR0179329 Zbl 0102.29301 |
| [a4] | P. Henrici, "Applied and computational complex analysis" , 1–3 , Wiley (1974–1986) MR1164865 MR1541308 MR1008928 MR0822470 MR0453984 MR0372162 Zbl 1107.30300 Zbl 0925.30003 Zbl 0635.30001 Zbl 0578.30001 Zbl 0363.30001 Zbl 0313.30001 |
| [a5] | E. Hille, "Analytic function theory" , 1–2 , Chelsea, reprint (1974) MR1532177 MR0201608 MR1530816 MR0107692 Zbl 0273.30002 Zbl 0102.29401 Zbl 0088.05204 |
| [a6] | Z. Nehari, "Conformal mapping" , Dover, reprint (1975) pp. 2 MR0377031 Zbl 0071.07301 Zbl 0052.08201 Zbl 0048.31503 Zbl 0041.41201 |
| [a7] | R. Nevanilinna, "Analytic functions" , Springer (1970) (Translated from German) |
| [a8] | R. Nevanlinna, V. Paatero, "Introduction to complex analysis" , Addison-Wesley (1969) (Translated from German) MR0239056 Zbl 0169.09001 |
| [a9] | W. Rudin, "Real and complex analysis" , McGraw-Hill (1974) pp. 24 MR0344043 Zbl 0278.26001 |
| [a10] | E.C. Titchmarsh, "The theory of functions" , Oxford Univ. Press (1939) MR0593142 MR0197687 MR1523319 Zbl 65.0302.01 |
| [a11] | H. Grauert, K. Fritzsche, "Several complex variables" , Springer (1976) (Translated from German) MR0414912 Zbl 0381.32001 |
| [a12] | H. Grauert, R. Remmert, "Theory of Stein spaces" , Springer (1979) (Translated from German) MR0580152 Zbl 0433.32007 |
| [a13] | R.C. Gunning, H. Rossi, "Analytic functions of several complex variables" , Prentice-Hall (1965) MR0180696 Zbl 0141.08601 |
| [a14] | G.M. [G.M. Khenkin] Henkin, J. Leiterer, "Theory of functions on complex manifolds" , Birkhäuser (1984) MR0795028 MR0774049 |
| [a15] | L. Hörmander, "An introduction to complex analysis in several variables" , North-Holland (1973) MR0344507 Zbl 0271.32001 |
| [a16] | S.G. Krantz, "Function theory of several complex variables" , Wiley (Interscience) (1982) MR0635928 Zbl 0471.32008 |
| [a17] | R. Narasimhan, "Several complex variables" , Univ. Chicago Press (1971) MR0342725 Zbl 0223.32001 |
| [a18] | W. Rudin, "Function theory in the unit ball in 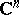 " , Springer (1980) MR601594 Zbl 0495.32001 " , Springer (1980) MR601594 Zbl 0495.32001 |
| [a19] | R.M. Range, "Holomorphic functions and integral representation in several complex variables" , Springer (1986) MR0847923 |
Analytic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Analytic_function&oldid=29387