Analytic continuation
of a function
An extension of a function 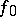 , already defined on a certain subset
, already defined on a certain subset 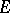 of a complex manifold
of a complex manifold 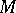 , to a function
, to a function 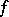 which is holomorphic on a certain domain
which is holomorphic on a certain domain  containing
containing 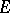 such that the restriction
such that the restriction 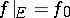 of
of 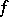 to
to 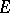 coincides with
coincides with 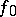 . The starting point in the theory of analytic continuation is the concept of an (analytic) element, i.e. a pair
. The starting point in the theory of analytic continuation is the concept of an (analytic) element, i.e. a pair 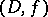 , where
, where 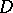 is a domain in
is a domain in 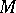 and
and 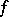 is a holomorphic function on
is a holomorphic function on 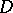 . One says that the elements
. One says that the elements 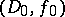 and
and 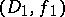 are direct analytic continuations of each other through a connected component
are direct analytic continuations of each other through a connected component 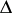 of the set
of the set 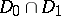 if
if 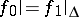 . By definition, an element
. By definition, an element 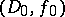 continues analytically to a boundary point
continues analytically to a boundary point 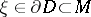 if there exists a direct analytic continuation
if there exists a direct analytic continuation 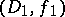 of the element
of the element  through
through 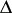 such that
such that 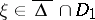 . A maximal analytic continuation of
. A maximal analytic continuation of 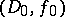 (in
(in  ) is an element
) is an element 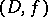 which continues
which continues 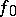 analytically to the domain
analytically to the domain 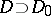 , but which cannot analytically be continued to any boundary point of
, but which cannot analytically be continued to any boundary point of 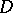 . The maximal analytic continuation of
. The maximal analytic continuation of 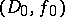 in
in  is unique, but does not always exist. In order to overcome this drawback one introduces the concept of a covering domain over
is unique, but does not always exist. In order to overcome this drawback one introduces the concept of a covering domain over 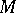 (a Riemann surface in the case
(a Riemann surface in the case 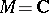 ), which is constructed from the elements that are analytic continuations of
), which is constructed from the elements that are analytic continuations of 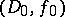 . An element
. An element 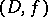 is called an analytic continuation of an element
is called an analytic continuation of an element 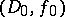 if there exists a finite chain of elements
if there exists a finite chain of elements 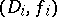 ,
,  , and corresponding connected components
, and corresponding connected components 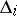 in
in 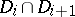 such that
such that 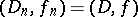 and
and 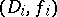 ,
, 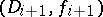 are direct analytic continuations of each other through
are direct analytic continuations of each other through 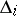 . One says that the holomorphic function
. One says that the holomorphic function 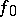 , initially defined in the domain
, initially defined in the domain 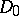 , continues analytically to a point
, continues analytically to a point 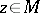 if there exists an analytic continuation
if there exists an analytic continuation 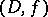 of
of 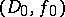 such that
such that 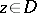 . One introduces an equivalence relation among the elements which are continuations of
. One introduces an equivalence relation among the elements which are continuations of 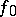 to the point
to the point 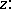
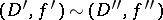 if
if 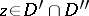 and
and 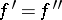 in a neighbourhood of
in a neighbourhood of  . On the set of equivalence classes
. On the set of equivalence classes 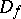 (for all possible
(for all possible  ) there is a natural way of introducing the topology and complex structure of a covering domain over
) there is a natural way of introducing the topology and complex structure of a covering domain over 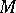 . The function
. The function 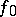 is lifted to
is lifted to 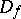 in a natural manner (its value on the equivalence class at
in a natural manner (its value on the equivalence class at  containing
containing 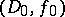 is set equal to
is set equal to  ); it continues analytically to all of
); it continues analytically to all of 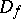 and, in the sense defined above, it does not continue to any boundary point of
and, in the sense defined above, it does not continue to any boundary point of 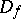 over
over 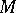 .
.
If 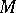 is the complex plane
is the complex plane  or, more generally, the complex space
or, more generally, the complex space 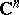 ,
, 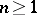 , this process of analytic continuation can be described more simply. A canonical element is a pair
, this process of analytic continuation can be described more simply. A canonical element is a pair 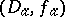 where
where 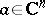 and
and 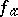 is a power series centred at the point
is a power series centred at the point  with a non-empty domain of convergence
with a non-empty domain of convergence 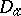 . A canonical element
. A canonical element 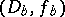 is an analytic continuation of
is an analytic continuation of 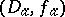 along a path
along a path 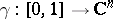 if there exists a family of canonical elements
if there exists a family of canonical elements 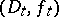 ,
, 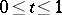 , with centres
, with centres 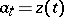 , such that
, such that 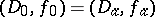 ,
,  , and for any
, and for any 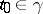 the elements
the elements 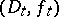 are direct analytic continuations of
are direct analytic continuations of 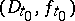 for all
for all 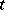 sufficiently near to
sufficiently near to 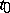 . The family
. The family 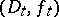 is in fact uniquely determined. If
is in fact uniquely determined. If 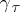 ,
, 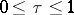 , is a continuous family of paths in
, is a continuous family of paths in 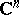 with common end points
with common end points  and
and 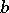 , and if
, and if 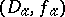 continues analytically along each
continues analytically along each 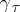 , then the result
, then the result 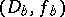 does not depend on
does not depend on  (the monodromy theorem). In the case of
(the monodromy theorem). In the case of 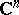 the canonical elements
the canonical elements 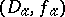 obtained by analytic continuation along all possible paths in
obtained by analytic continuation along all possible paths in 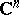 become the points of
become the points of 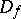 ;
; 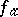 is lifted to
is lifted to 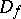 and continues analytically throughout
and continues analytically throughout 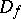 to a holomorphic function
to a holomorphic function 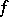 , while
, while 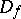 is the domain of holomorphy of
is the domain of holomorphy of 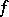 .
.
This general process of analytic continuation is not very effective in practice, and for this reason many special methods of analytic continuation are employed. These include various analytic representations: parameter-dependent integrals such as Cauchy-type integrals (cf. Cauchy integral); the Laplace integral; the Borel transform; change of variable in a power series, special methods of summation of power series (the Borel expansion into a polynomial series converging in a maximal polygon (cf. Borel summation method), the Mittag-Leffler series converging in a maximal star (cf. Star of a function element; Mittag-Leffler summation method), etc., the Riemann–Schwarz reflection method (cf. Riemann–Schwarz principle), functional and differential equations satisfied by a function (e.g. the equation 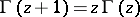 for the gamma-function, conditions of periodicity, evenness, symmetry, etc.), and analytic expressions in terms of known functions.
for the gamma-function, conditions of periodicity, evenness, symmetry, etc.), and analytic expressions in terms of known functions.
The subject of analytic continuation also comprises studies on the relation between the initial element of an analytic function (a Taylor series) and the properties of the complete analytic function generated by this element [1]. Results have been obtained on singular points (criteria for singular points, the Hadamard theorem on products, the Fabry theorem on quotients) and on singular curves (theorems on gaps and non-extendability beyond the boundary of the disc of convergence, e.g. the Hadamard theorem on gaps, the Fabry theorem on gaps, etc.), theorems on over-convergence and on relations between analytic continuation of a power series and properties of an entire function which defines its coefficients, problems of meromorphic continuation, meromorphic continuation by Padé approximation, etc. The field of analytic continuation also includes theorems on removable singularities (removability of an isolated singularity of a bounded holomorphic function, removability of a rectifiable singular curve under conditions of continuity, etc.), as well as a large class of theorems on the simultaneous continuation of holomorphic functions of several complex variables. The space 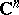 ,
, 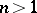 , comprises domains for which every holomorphic function can be extended to a larger domain (this phenomenon is absent in the one-dimensional case). It is therefore an important problem in the theory of analytic continuation of functions of several complex variables to describe these larger domains — the so-called envelopes of holomorphy. Thus, there are descriptions of the hulls (envelopes) of holomorphy for Hartogs domains,
, comprises domains for which every holomorphic function can be extended to a larger domain (this phenomenon is absent in the one-dimensional case). It is therefore an important problem in the theory of analytic continuation of functions of several complex variables to describe these larger domains — the so-called envelopes of holomorphy. Thus, there are descriptions of the hulls (envelopes) of holomorphy for Hartogs domains,  -circular and tube domains, theorems on the removability of compact singularity sets and of singularity sets of codimension
-circular and tube domains, theorems on the removability of compact singularity sets and of singularity sets of codimension 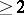 , the Bogolyubov theorem on the "edge-of-the-wedge" and
, the Bogolyubov theorem on the "edge-of-the-wedge" and
P Vladimirov's theorem on 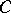 -convex hulls [3] (cf. Holomorphic envelope; Hartogs domain; Tube domain). A number of effective methods for the construction of envelopes of holomorphy are available [3].
-convex hulls [3] (cf. Holomorphic envelope; Hartogs domain; Tube domain). A number of effective methods for the construction of envelopes of holomorphy are available [3].
The problem of analytic continuation of functions of a real variable can be reduced to that of holomorphic functions, since for any domain 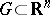 and any function
and any function 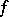 analytic in
analytic in 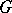 there are a domain
there are a domain 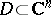 and a function
and a function 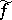 holomorphic in
holomorphic in 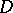 such that
such that 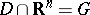 and
and 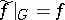 .
.
References
| [1] | L. Bieberbach, "Analytische Fortsetzung" , Springer (1955) pp. Sect. 3 |
| [2] | A.I. Markushevich, "Theory of functions of a complex variable" , 1–3 , Chelsea (1977) (Translated from Russian) |
| [3] | V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) (Translated from Russian) |
Comments
References
| [a1] | L. Hörmander, "An introduction to complex analysis in several variables" , v. Nostrand (1966) |
| [a2] | H. Grauert, K. Fritzsche, "Several complex variables" , Springer (1976) (Translated from German) |
Analytic continuation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Analytic_continuation&oldid=18376