Analytic capacity
analytic measure, Ahlfors analytic measure
A set function in the plane, introduced by L. Ahlfors [1], which is an analogue of the logarithmic capacity, and which is suited for the characterization of sets of removable singularities of bounded analytic functions. Let 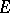 be a bounded closed set in the plane, let
be a bounded closed set in the plane, let 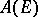 be the set of functions which are analytic outside
be the set of functions which are analytic outside 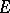 , vanish at infinity and are bounded everywhere outside
, vanish at infinity and are bounded everywhere outside 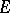 by the constant 1. Let
by the constant 1. Let 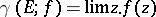 as
as 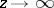 . The number
. The number 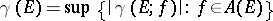 , is called the analytic capacity of the set
, is called the analytic capacity of the set 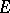 . The analytic capacity of an arbitrary set is usually defined as the supremum of the analytic capacities of its bounded closed subsets.
. The analytic capacity of an arbitrary set is usually defined as the supremum of the analytic capacities of its bounded closed subsets.
If 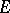 is a bounded closed set, then a necessary and sufficient condition in order that each function which is analytic and bounded outside
is a bounded closed set, then a necessary and sufficient condition in order that each function which is analytic and bounded outside 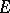 be extendable to
be extendable to  , is that the analytic capacity of
, is that the analytic capacity of 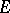 be zero (the Ahlfors theorem).
be zero (the Ahlfors theorem).
There also exist several concepts related to analytic capacity which are suited to the metrics of various other spaces of analytic functions (see, for example, [2] and [3]).
The concept of analytic capacity proved to be well suited to certain problems in approximation theory, where the solution of a number of fundamental problems is formulated in terms of analytic capacity. Thus, [4], any continuous function on a bounded closed set 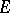 in the plane can be uniformly approximated by rational functions to any desired degree of accuracy, if and only if the equality
in the plane can be uniformly approximated by rational functions to any desired degree of accuracy, if and only if the equality
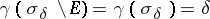 |
holds for any disc 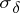 of radius
of radius 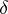 .
.
References
| [1] | L.V. Ahlfors, "Bounded analytic functions" Duke Math. J. , 14 (1947) pp. 1–11 |
| [2] | P.R. Garabedian, "The classes 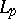 and conformal mapping" Trans. Amer. Math. Soc. , 69 (1950) pp. 392–415 and conformal mapping" Trans. Amer. Math. Soc. , 69 (1950) pp. 392–415 |
| [3] | S.O. Sinanyan, "Approximation by analytic functions and polynomials in a real mean" Dokl. Akad. Nauk ArmSSR , 35 : 3 (1962) pp. 107–112 (In Russian) |
| [4] | A.G. Vitushkin, "Analytic capacity of sets in problems of approximation theory" Russian Math. Surveys , 22 : 6 (1967) pp. 139–200 Uspekhi Mat. Nauk , 22 : 6 (1967) pp. 141–199 |
Comments
A good reference to the general area is [a1].
References
| [a1] | T.W. Gamelin, "Uniform algebras" , Prentice-Hall (1969) |
Analytic capacity. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Analytic_capacity&oldid=11845