Amplitude of an elliptic integral
From Encyclopedia of Mathematics
The variable  , considered as a function of
, considered as a function of  , in an elliptic integral of the first kind
, in an elliptic integral of the first kind
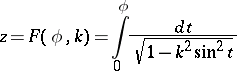 |
in the normal Legendre form. The concept of the amplitude of an elliptic integral and the notation  were introduced by C.G.J. Jacobi in 1829. The amplitude of an elliptic integral is an infinite-valued periodic function of
were introduced by C.G.J. Jacobi in 1829. The amplitude of an elliptic integral is an infinite-valued periodic function of  . The basic elliptic Jacobi functions
. The basic elliptic Jacobi functions  ,
,  ,
,  are all single-valued. It is convenient, however (e.g. for purposes of tabulation), to consider an elliptic integral as a function
are all single-valued. It is convenient, however (e.g. for purposes of tabulation), to consider an elliptic integral as a function  of the amplitude
of the amplitude 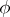 and the modulus
and the modulus 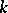 . See also Jacobi elliptic functions.
. See also Jacobi elliptic functions.
How to Cite This Entry:
Amplitude of an elliptic integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Amplitude_of_an_elliptic_integral&oldid=13707
Amplitude of an elliptic integral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Amplitude_of_an_elliptic_integral&oldid=13707
This article was adapted from an original article by E.D. Solomentsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article