Amalgam of groups
A family of groups  , that satisfies the condition that the intersection
, that satisfies the condition that the intersection  is a subgroup in
is a subgroup in  and
and  for any
for any  from
from  . An example of an amalgam of groups is an arbitrary family of subgroups of a given group. An imbedding of an amalgam of groups
. An example of an amalgam of groups is an arbitrary family of subgroups of a given group. An imbedding of an amalgam of groups  into a group
into a group  is a one-to-one mapping of the union
is a one-to-one mapping of the union  into
into 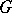 whose restriction to each
whose restriction to each 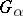 is an isomorphism. An amalgam of groups in which all intersections
is an isomorphism. An amalgam of groups in which all intersections 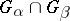 are identical (and equal to, say, a subgroup
are identical (and equal to, say, a subgroup 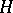 ) is imbeddable in the group that is the free product of the groups
) is imbeddable in the group that is the free product of the groups  with the amalgamated subgroup
with the amalgamated subgroup  . On the other hand, there exists an amalgam of four Abelian groups that is not imbeddable in a group. The principal problem concerning amalgams of groups is, generally speaking, as follows. Let
. On the other hand, there exists an amalgam of four Abelian groups that is not imbeddable in a group. The principal problem concerning amalgams of groups is, generally speaking, as follows. Let 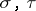 be possible properties of groups. The question to be answered is the nature of the conditions under which an amalgam of groups with the property
be possible properties of groups. The question to be answered is the nature of the conditions under which an amalgam of groups with the property 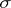 is imbeddable in a group with the property
is imbeddable in a group with the property  . It was found that all amalgams of two finite groups are imbeddable in a finite group. An amalgam of three Abelian groups is imbeddable in an Abelian group. An amalgam of four Abelian groups imbedded in a group is contained in an Abelian group. There exists an amalgam of five Abelian groups which is imbeddable in a group, but not in an Abelian group. Another problem that has been studied is the imbeddability of an amalgam of groups if
. It was found that all amalgams of two finite groups are imbeddable in a finite group. An amalgam of three Abelian groups is imbeddable in an Abelian group. An amalgam of four Abelian groups imbedded in a group is contained in an Abelian group. There exists an amalgam of five Abelian groups which is imbeddable in a group, but not in an Abelian group. Another problem that has been studied is the imbeddability of an amalgam of groups if  denote solvability, nilpotency, periodicity, local finiteness, etc. (in different combinations).
denote solvability, nilpotency, periodicity, local finiteness, etc. (in different combinations).
Comments
In the definition of amalgam above, think of the 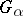 as all being subsets of some large set
as all being subsets of some large set  . The amalgamated product of groups
. The amalgamated product of groups 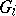 "over a common subgroup U" is constructed as follows. Let
"over a common subgroup U" is constructed as follows. Let  be a set of groups indexed by the set
be a set of groups indexed by the set  . For each
. For each  let
let  be a subgroup of
be a subgroup of 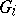 and for each
and for each 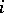 let there be an isomorphism
let there be an isomorphism 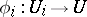 identifying
identifying 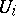 and
and 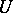 . Consider the set
. Consider the set 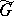 of all words
of all words
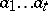 |
with each 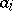 from some
from some 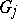 , and consider the following elementary equivalences
, and consider the following elementary equivalences
1) if 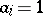 then
then  is equivalent to
is equivalent to 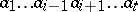 ;
;
2) if 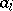 and
and 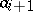 belong to the same group
belong to the same group  and
and 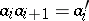 in
in 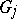 then
then 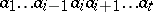 is equivalent to
is equivalent to 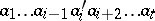 ;
;
3) if 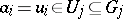 and
and 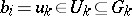 and
and 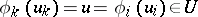 , then
, then  is equivalent to
is equivalent to  .
.
Let 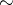 be the equivalence relation generated by these elementary equivalences, then
be the equivalence relation generated by these elementary equivalences, then  is the amalgamated product of the
is the amalgamated product of the 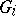 , more precisely of the
, more precisely of the  (i.e. the free product with amalgamated subgroup of the
(i.e. the free product with amalgamated subgroup of the 
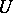 ); the group law is induced by concatenation.
); the group law is induced by concatenation.
Amalgamated products are non-trivial. This follows from the following canonical form theorem. For each 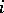 select a set
select a set  of left coset representatives of
of left coset representatives of 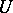 in
in 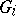 . Then each word is equivalent to precisely one of the form
. Then each word is equivalent to precisely one of the form 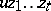 with each
with each 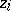 in some
in some 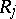 ,
, 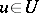 and
and  and
and 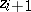 belonging to different
belonging to different 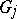 's for
's for 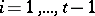 . If
. If  one obtains of course the free product of the
one obtains of course the free product of the  . A subgroup of a free product is itself a free product (Kurosh' theorem). Subgroups of a product with an amalgamated subgroup need not be themselves of this type. The reason is that if
. A subgroup of a free product is itself a free product (Kurosh' theorem). Subgroups of a product with an amalgamated subgroup need not be themselves of this type. The reason is that if 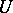 is the amalgamated subgroup, then one can take subgroups
is the amalgamated subgroup, then one can take subgroups 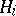 of the
of the 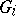 with different intersections with
with different intersections with 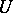 so that the
so that the 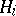 will amalgamate in various different ways. This leads to generalized amalgamated products and the notion of amalgam as defined above. The theory of these is still incomplete.
will amalgamate in various different ways. This leads to generalized amalgamated products and the notion of amalgam as defined above. The theory of these is still incomplete.
References
| [a1] | M. Hall jr., "The theory of groups" , Macmillan (1959) |
| [a2] | H. Neumann, "Generalized free products with amalgamated subgroups I" Amer. J. Math. , 70 (1948) pp. 590–625 |
| [a3] | H. Neumann, "Generalized free products with amalgamated subgroups II" Amer. J. Math. , 71 (1949) pp. 491–540 |
Amalgam of groups. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Amalgam_of_groups&oldid=12238