Alternion
A hypercomplex number. Alternions may be considered as a generalization of the complex numbers, double numbers (cf. Double and dual numbers) and quaternions. The algebra 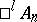 of alternions of order
of alternions of order  and of index
and of index 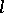 is an algebra of dimension
is an algebra of dimension 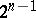 over the field of real numbers, with unit element 1 and a system of generators
over the field of real numbers, with unit element 1 and a system of generators 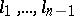 , in which the multiplication satisfies the formula
, in which the multiplication satisfies the formula
 |
where 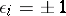 , the value
, the value 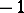 occurs
occurs 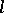 times and
times and 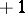 occurs
occurs 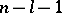 times, respectively. A base of the algebra is formed by the unit element and by elements of the form
times, respectively. A base of the algebra is formed by the unit element and by elements of the form
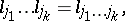 |
where 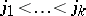 . In this base any alternion
. In this base any alternion 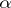 can be written as
can be written as
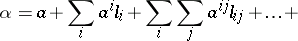 |
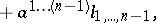 |
where 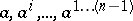 are real numbers. The alternion
are real numbers. The alternion 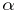 conjugate to the alternion
conjugate to the alternion 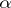 is defined by the formula
is defined by the formula
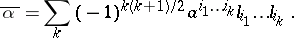 |
The following equalities hold
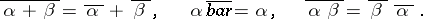 |
The product 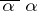 is always a positive real number; the quantity
is always a positive real number; the quantity 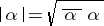 is called the modulus of the alternion
is called the modulus of the alternion 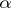 . If the number
. If the number 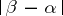 is taken as the distance between two alternions
is taken as the distance between two alternions  and
and  , then the algebras
, then the algebras 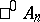 and
and 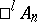 ,
, 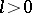 , are isometric to the Euclidean space
, are isometric to the Euclidean space 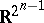 and the pseudo-Euclidean spaces
and the pseudo-Euclidean spaces 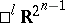 , respectively. The algebra
, respectively. The algebra 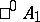 is isomorphic to the field of real numbers;
is isomorphic to the field of real numbers; 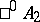 is isomorphic to the field of complex numbers;
is isomorphic to the field of complex numbers; 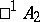 is isomorphic to the algebra of double numbers;
is isomorphic to the algebra of double numbers; 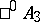 is isomorphic to the skew-field of quaternions; and
is isomorphic to the skew-field of quaternions; and 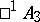 and
and 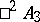 are isomorphic to the so-called algebras of anti-quaternions. The elements of
are isomorphic to the so-called algebras of anti-quaternions. The elements of 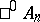 are the so-called Clifford numbers. The algebra
are the so-called Clifford numbers. The algebra 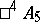 was studied by P. Dirac in the context of the spin of an electron.
was studied by P. Dirac in the context of the spin of an electron.
The algebras of alternions are special cases of Clifford algebras (cf. Clifford algebra).
References
| [1] | B.A. Rozenfel'd, "Non-Euclidean geometry" , Moscow (1955) (In Russian) |
Alternion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Alternion&oldid=15232