Alternating-direction implicit method
A method introduced in 1955 by D.W. Peaceman and H.H. Rachford [a3] and J. Douglas [a1] as a technique for the numerical solution of elliptic and parabolic differential equations (cf. Elliptic partial differential equation; Parabolic partial differential equation). Let  be a bounded region and
be a bounded region and 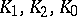 continuous functions with
continuous functions with 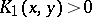 ,
, 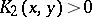 ,
, 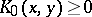 in
in  . The discretization of the elliptic boundary value problem (cf. Boundary value problem, elliptic equations)
. The discretization of the elliptic boundary value problem (cf. Boundary value problem, elliptic equations)
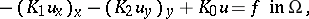 |
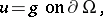 |
in a bounded region 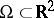 by finite differences leads to a system of linear equations of the form
by finite differences leads to a system of linear equations of the form
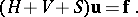 |
Here, the matrices 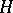 and
and 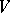 stand for the discretization of the differential operators in the
stand for the discretization of the differential operators in the  (horizontal) and
(horizontal) and 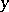 (vertical) direction, respectively, and
(vertical) direction, respectively, and 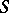 is a diagonal matrix representing multiplication by
is a diagonal matrix representing multiplication by 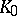 . The alternating-direction implicit method attempts to solve this linear system by the iteration
. The alternating-direction implicit method attempts to solve this linear system by the iteration
 |
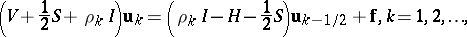 |
with some parameters 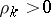 . On a uniform mesh, each of the two half-steps in the above iteration scheme requires the solution of a number of tri-diagonal systems arising from one-dimensional difference operators, a task which is relatively inexpensive. On an
. On a uniform mesh, each of the two half-steps in the above iteration scheme requires the solution of a number of tri-diagonal systems arising from one-dimensional difference operators, a task which is relatively inexpensive. On an  by
by  rectangular mesh, the appropriate choice of a set of parameters
rectangular mesh, the appropriate choice of a set of parameters 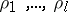 (with
(with 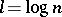 ) in the above iteration allows one to solve the Poisson equation (
) in the above iteration allows one to solve the Poisson equation (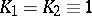 ,
, 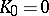 ) with an operation count of
) with an operation count of 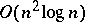 , which is almost optimal. (Optimal methods with an operation count proportional to the number of unknowns
, which is almost optimal. (Optimal methods with an operation count proportional to the number of unknowns 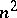 have later been developed using multi-grid methods.)
have later been developed using multi-grid methods.)
For the parabolic initial-boundary value problem
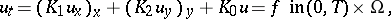 |
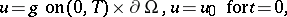 |
implicit discretization in time requires the solution of an elliptic boundary value problem of the type above in each time-step. The alternating-direction implicit method advances in time by inverting only the one-dimensional difference operators in  - and in
- and in 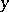 -direction. Each time step is therefore much less expensive. It can be shown to be unconditionally stable. The classical reference is [a4], Chapts. 7, 8.
-direction. Each time step is therefore much less expensive. It can be shown to be unconditionally stable. The classical reference is [a4], Chapts. 7, 8.
In the 1980{}s, the apparent potential for parallelism in the alternating-direction implicit method led to research on the appropriate implementation on parallel computers [a2].
References
| [a1] | J. Douglas, "On the numerical integration of 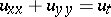 by implicit methods" SIAM J. , 3 (1962) pp. 42–65 by implicit methods" SIAM J. , 3 (1962) pp. 42–65 |
| [a2] | S. Lennart Johnsson, Y. Saad, M.H. Schultz, "Alternating direction methods on multiprocessors" SIAM J. Sci. Statist. Comput. , 8 (1987) pp. 686–700 |
| [a3] | D.W. Peaceman, H.H. Rachford, "The numerical solution of parabolic and elliptic differential equations" SIAM J. , 3 (1955) pp. 28–41 |
| [a4] | R.S. Varga, "Matrix iterative analysis" , Prentice-Hall (1962) |
Alternating-direction implicit method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Alternating-direction_implicit_method&oldid=14574