Almost-periodic function on a group
A generalization of almost-periodic functions defined on 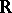 . Let
. Let 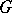 be an (abstract) group. A bounded complex-valued function
be an (abstract) group. A bounded complex-valued function 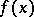 ,
, 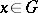 , is called a right almost-periodic function if the family
, is called a right almost-periodic function if the family 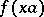 , where
, where  runs through the entire group
runs through the entire group 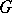 , is (relatively) compact in the topology of uniform convergence on
, is (relatively) compact in the topology of uniform convergence on  , i.e. if every sequence of functions
, i.e. if every sequence of functions 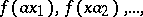 contains a subsequence which is uniformly convergent on
contains a subsequence which is uniformly convergent on  . A left almost-periodic function on
. A left almost-periodic function on 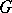 is defined similarly. It turns out that every right (left) almost-periodic function
is defined similarly. It turns out that every right (left) almost-periodic function 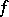 is also left (right) almost-periodic, and the family
is also left (right) almost-periodic, and the family 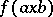 , where
, where  and
and 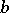 independently run through
independently run through 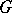 , is (relatively) compact. The latter property is often taken as a definition of almost-periodic functions on
, is (relatively) compact. The latter property is often taken as a definition of almost-periodic functions on 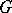 . The set of all almost-periodic functions on
. The set of all almost-periodic functions on 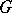 is a Banach space with a norm
is a Banach space with a norm 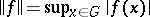 .
.
The theory of almost-periodic functions on a group depends essentially on the mean-value theorem (cf. [5], [8]). A linear functional 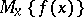 defined on the space of almost-periodic functions is called a mean value if
defined on the space of almost-periodic functions is called a mean value if
1) 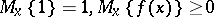 for
for 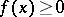 and
and 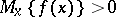 for
for 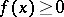 ,
, 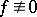 ;
;
2) 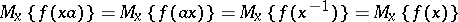 , for all
, for all 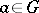 .
.
A unitary matrix function 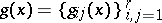 , defined on
, defined on  , is called a unitary representation of
, is called a unitary representation of 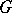 if
if 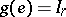 (
( is the identity element of
is the identity element of 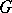 and
and 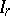 is the identity matrix of order
is the identity matrix of order  ) and if for all
) and if for all 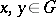 ,
, 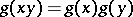 . The number
. The number  is called the dimension of the representation
is called the dimension of the representation 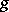 . The matrix entries
. The matrix entries 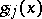 are almost-periodic functions on
are almost-periodic functions on 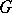 . In the theory of almost-periodic functions on a group they play the same role as the functions
. In the theory of almost-periodic functions on a group they play the same role as the functions 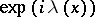 in the theory of almost-periodic functions on
in the theory of almost-periodic functions on 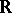 .
.
Two representations 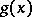 and
and 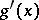 are said to be equivalent if a constant matrix
are said to be equivalent if a constant matrix 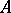 exists such that
exists such that 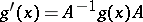 . A representation
. A representation 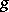 is said to be irreducible if the family of the matrices
is said to be irreducible if the family of the matrices 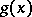 ,
, 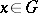 , does not admit a common non-trivial subspace in
, does not admit a common non-trivial subspace in 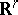 . The set of all irreducible unitary representations is partitioned into classes of mutually-equivalent representations. Let one representation be chosen from each equivalence class and let the set thus obtained be denoted by
. The set of all irreducible unitary representations is partitioned into classes of mutually-equivalent representations. Let one representation be chosen from each equivalence class and let the set thus obtained be denoted by 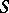 . Then the set of almost-periodic functions
. Then the set of almost-periodic functions
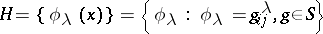 |
on 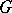 turns out to be an orthogonal (though, in general, uncountable) system with respect to the mean value.
turns out to be an orthogonal (though, in general, uncountable) system with respect to the mean value.
Theorem 1 (the Parseval equality). For an almost-periodic function  the following equality holds:
the following equality holds:
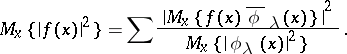 |
(Thus, for only countably many 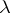 ,
, 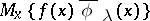 differs from zero; the series
differs from zero; the series
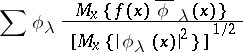 |
is called the Fourier series of 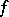 .
.
A representation 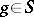 is said to occur in the Fourier series of an almost-periodic function
is said to occur in the Fourier series of an almost-periodic function 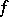 if
if  for some
for some 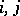 ,
, 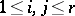 .
.
Theorem 2 (the approximation theorem). The set 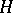 is dense in the space of almost-periodic functions equipped with the norm
is dense in the space of almost-periodic functions equipped with the norm
 |
and every almost-periodic function can be arbitrarily well approximated by a finite linear combination of matrix entries of representations occurring in its Fourier series.
If  is a topological group, then to the definition of an almost-periodic function should be added the requirement of its continuity. In this case, the representations occurring in its Fourier series are also continuous.
is a topological group, then to the definition of an almost-periodic function should be added the requirement of its continuity. In this case, the representations occurring in its Fourier series are also continuous.
If  is an Abelian group, then the continuous unitary representations are one-dimensional. They are called the characters of
is an Abelian group, then the continuous unitary representations are one-dimensional. They are called the characters of  . The characters of
. The characters of  are denoted by
are denoted by 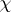 and Parseval's equality reads as follows:
and Parseval's equality reads as follows:
 |
In the case 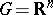 the continuous characters are the functions
the continuous characters are the functions 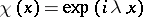 , where
, where  ,
,  . Theorems 1 and 2 imply the main results in the theory of almost-periodic functions of a single or of several variables.
. Theorems 1 and 2 imply the main results in the theory of almost-periodic functions of a single or of several variables.
The proof of the main statements in the theory of almost-periodic functions is based on the consideration of integral equations on a group (cf. [2]). The existence of sufficiently many linear representations of compact Lie groups has been proved [3]. In this case, invariant integration (and consequently, the mean) can be established directly. Invariant integration on an abstract compact group has been constructed [4] depending on an extension of the Peter–Weyl theory to this case.
The theory of almost-periodic functions on a group can be deduced (cf. [3]) from the Peter–Weyl theory in the following way. Let 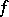 be an almost-periodic function on a group
be an almost-periodic function on a group 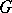 and let
and let
 |
Then the set 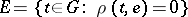 is a normal subgroup of
is a normal subgroup of 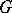 ,
, 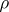 is an invariant metric on the quotient group
is an invariant metric on the quotient group 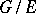 and
and 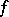 is uniformly continuous on
is uniformly continuous on 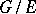 .
.
The almost-periodicity of  implies that the completion of
implies that the completion of  in the metric
in the metric 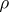 is a compact group and Theorems 1 and 2 follow from the Peter–Weyl theory.
is a compact group and Theorems 1 and 2 follow from the Peter–Weyl theory.
References
| [1] | B.M. Levitan, "Almost-periodic functions" , Moscow (1953) pp. Chapt. 6 (In Russian) |
| [2] | H. Weyl, "Integralgleichungen und fastperiodische Funktionen" Math. Ann. , 97 (1927) pp. 338–356 |
| [3] | F. Peter, H. Weyl, "Die Vollständigkeit der primitiven Darstellungen einer geschlossener kontinuierlichen Gruppe" Math. Ann. , 97 (1927) pp. 737–755 |
| [4] | J. von Neumann, "Zum Haarschen Mass in topologischen Gruppen" Compositio Math. , 1 (1934) pp. 106–114 |
| [5] | J. von Neumann, "Almost periodic functions in a group I" Trans. Amer. Math. Soc. , 36 (1934) pp. 445–492 |
| [6] | A. Weil, C.R. Acad. Sci. Paris Sér. I Math. , 200 (1935) pp. 38–40 |
| [7] | K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, Sect. 4; 5 |
| [8] | W. Maak, "Fastperiodische Funktionen" , Springer (1950) |
Comments
Instead of the term "mean value" one often uses the term "invariant-mean functional for almost-periodic functions43A07invariant mean" (cf. [a1], Sect. 18).
For an Abelian group 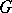 the uniformly almost-periodic functions are precisely those that can be continuously extended to the Bohr compactification of
the uniformly almost-periodic functions are precisely those that can be continuously extended to the Bohr compactification of 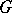 .
.
A unified account of the theory of almost-periodic functions on groups can also be found in [a2] and [a3], Sect. 41. The basic observation is that the Banach algebra of (continuous) almost-periodic functions on a (topological) group 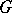 is isomorphic to the Banach algebra of all continuous functions on the so-called Bohr compactification
is isomorphic to the Banach algebra of all continuous functions on the so-called Bohr compactification 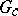 of
of 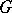 . In this way the theory is reduced to the theory of continuous functions on a compact group (e.g., the mean-value theorem corresponds to the normalized Haar measure on
. In this way the theory is reduced to the theory of continuous functions on a compact group (e.g., the mean-value theorem corresponds to the normalized Haar measure on 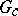 , the approximation theorem is nothing else than the well-known Peter–Weyl theorem for compact groups, etc.). The Bohr compactification of
, the approximation theorem is nothing else than the well-known Peter–Weyl theorem for compact groups, etc.). The Bohr compactification of 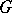 can be characterized as the reflection of
can be characterized as the reflection of 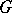 in the subcategory of all compact groups. By considering reflections in other subcategories of the category of all topological groups (or even of all semi-topological semi-groups) one can define other classes of almost-periodic functions on groups (or semi-groups), see [a4]. Weakly almost-periodic functions are of particular interest in functional-analytic applications (semi-groups of operators). See also [7] and [a5].
in the subcategory of all compact groups. By considering reflections in other subcategories of the category of all topological groups (or even of all semi-topological semi-groups) one can define other classes of almost-periodic functions on groups (or semi-groups), see [a4]. Weakly almost-periodic functions are of particular interest in functional-analytic applications (semi-groups of operators). See also [7] and [a5].
References
| [a1] | E. Hewitt, K.A. Ross, "Abstract harmonic analysis" , 1 , Springer (1979) |
| [a2] | A. Weil, "l'Intégration dans les groupes topologiques et ses applications" , Hermann (1940) |
| [a3] | L.H. Loomis, "An introduction to abstract harmonic analysis" , v. Nostrand (1953) |
| [a4] | J.F. Berglund, H.D. Junghen, P. Milnes, , Compact right to topological semigroups and generalizations of almost periodicity , Lect. notes in math. , 663 , Springer (1978) |
| [a5] | R.B. Burckel, "Weakly almost periodic functions on semi-groups" , Gordon & Breach (1970) |
| [a6] | C. Corduneanu, "Almost periodic functions" , Interscience (1961) pp. Chapt. 7 |
| [a7] | I. Glicksberg, K. de Leeuw, "Almost periodic functions on semigroups" Acta Math. , 105 (1961) pp. 99–140 |
| [a8] | L. Amerio, G. Prouse, "Almost-periodic functions and functional equations" , v. Nostrand (1971) |
| [a9] | J. Dixmier, "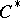 algebras" , North-Holland (1977) (Translated from French) algebras" , North-Holland (1977) (Translated from French) |
Almost-periodic function on a group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Almost-periodic_function_on_a_group&oldid=13583