Almost-periodic analytic function
An analytic function $f(s)$,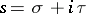 , regular in a strip
, regular in a strip 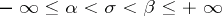 , and expandable into a series
, and expandable into a series
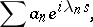 |
where the 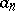 are complex and the
are complex and the 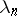 are real numbers. A real number
are real numbers. A real number  is called an
is called an  -almost-period of
-almost-period of 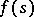 if for all points of the strip
if for all points of the strip 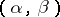 the inequality
the inequality
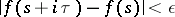 |
holds. An almost-periodic analytic function is an analytic function that is regular in a strip 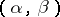 and possesses a relatively-dense set of
and possesses a relatively-dense set of  -almost-periods for every
-almost-periods for every 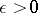 . An almost-periodic analytic function on a closed strip
. An almost-periodic analytic function on a closed strip 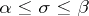 is defined similarly. An almost-periodic analytic function on a strip
is defined similarly. An almost-periodic analytic function on a strip 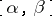 is a uniformly almost-periodic function of the real variable
is a uniformly almost-periodic function of the real variable  on every straight line in the strip and it is bounded in
on every straight line in the strip and it is bounded in 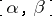 , i.e. on any interior strip. If a function
, i.e. on any interior strip. If a function 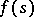 , regular in a strip
, regular in a strip 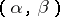 , is a uniformly almost-periodic function on at least one line
, is a uniformly almost-periodic function on at least one line 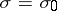 in the strip, then boundedness of
in the strip, then boundedness of 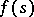 in
in 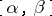 implies its almost-periodicity on the entire strip
implies its almost-periodicity on the entire strip 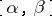 . Consequently, the theory of almost-periodic analytic functions turns out to be a theory analogous to that of almost-periodic functions of a real variable (cf. almost-periodic function). Therefore, many important results of the latter theory can be easily carried over to almost-periodic analytic functions: the uniqueness theorem, Parseval's equality, rules of operation with Dirichlet series, the approximation theorem, and several other theorems.
. Consequently, the theory of almost-periodic analytic functions turns out to be a theory analogous to that of almost-periodic functions of a real variable (cf. almost-periodic function). Therefore, many important results of the latter theory can be easily carried over to almost-periodic analytic functions: the uniqueness theorem, Parseval's equality, rules of operation with Dirichlet series, the approximation theorem, and several other theorems.
References
| [1] | H. Bohr, "Almost-periodic functions" , Chelsea, reprint (1947) (Translated from German) |
| [2] | B.M. Levitan, "Almost-periodic functions" , Moscow (1953) pp. Chapt. 7 (In Russian) |
Comments
The hyphen between almost and periodic is sometimes dropped.
References
| [a1] | C. Corduneanu, "Almost periodic functions" , Interscience (1961) pp. Chapt. 3 |
Almost-periodic analytic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Almost-periodic_analytic_function&oldid=29514